NEET-XII-Physics
31: Capacitors
- #21The particle P shown in figure (31-E11) has a mass of 10 mg and a charge of -0⋅01 µC. Each plate has a surface area 100 cm2 on one side. What potential difference V should be applied to the combination to hold the particle P in equilibrium?
Figure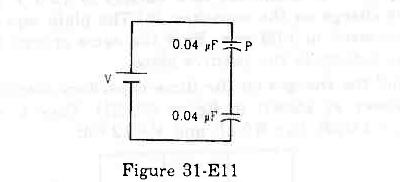 Ans : The particle is balanced when the electrical force on it is balanced by its weight.
Ans : The particle is balanced when the electrical force on it is balanced by its weight.
Thus,
`` mg=qE``
`` mg=q\times \frac{V\text{'}}{d}...\left(\,\mathrm{\,i\,}\right)``
`` ``
Here,
d = Separation between the plates of the capacitor
V' = Potential difference across the capacitor containing the particle
We know that the capacitance of a capacitor is given by
`` C=\frac{{\in }_{0}A}{d}``
`` \Rightarrow d=\frac{{\in }_{0}A}{C}``
Thus, eq. (i) becomes
`` mg=q\times V\text{'}\times \frac{\,\mathrm{\,C\,}}{{\in }_{0}A}``
`` \Rightarrow V\text{'}=\frac{mg{\in }_{0}A}{q\times C}``
`` \Rightarrow V\text{'}=\frac{{10}^{-6}\times 9.8\times (8.85\times {10}^{-12})\times (100\times {10}^{-4})}{(0.01\times {10}^{-6})\times (0.04\times {10}^{-6})}``
`` \Rightarrow V\text{'}=21.68\,\mathrm{\,mV\,}``
Since the values of both the capacitors are the same,
V = 2V' = 2 `` \times `` 21.86 `` \approx `` 43 mV
Page No 166: