HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

29: Electric Field and Potential

with Solutions - page 4
Qstn# iv-22 Prvs-QstnNext-Qstn
  • #22
    Two identical balls, each with a charge of 2.00 × 10-7 C and a mass of 100 g, are suspended from a common point by two insulating strings, each 50 cm long. The balls are held 5.0 cm apart and then released. Find (a) the electric force on one of the charged balls (b) the components of the resultant force on it along and perpendicular to the string (c) the tension in the string (d) the acceleration of one of the balls.
    Answers are to be obtained only for the instant just after the release. (a) the electric force on one of the charged balls (b) the components of the resultant force on it along and perpendicular to the string (c) the tension in the string (d) the acceleration of one of the balls.
    Answers are to be obtained only for the instant just after the release.
    Ans : Given:
    Magnitude of the charges, q = 2.0 × 10-7 C
    Separation between the charges, `` r=5\times {10}^{-2}\,\mathrm{\,m\,}``
    Length of the string, `` l=50\,\mathrm{\,cm\,}=50\times {10}^{-2}\,\mathrm{\,m\,}``
    Mass of the balls, m = 100 g = 0.1 kg
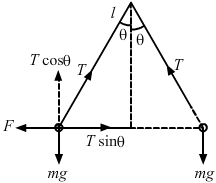    (a) By Coulomb's Law, the electric force,
    `` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}^{2}}{{r}^{2}}``
    `` =14.4\,\mathrm{\,N\,}\times {10}^{-2}\,\mathrm{\,N\,}``
    `` =0.144\,\mathrm{\,N\,}`` (b) The components of the resultant force along it is zero because mg balances Tcosθ, as shown in the figure. So,
    F = Tsinθ (c) Tension in the string,
    Tsinθ = F ..(1)
    Tcosθ = mg ...(2)
    Squaring equations (1) and (2) and adding, we get
    `` {T}^{2}={F}^{2}+{\left(mg\right)}^{2}``
    `` ={\left(0.144\right)}^{2}+{\left(0.1\times 9.8\right)}^{2}``
    `` \Rightarrow T=0.986\,\mathrm{\,N\,}`` (d) --
    Page No 121: (a) By Coulomb's Law, the electric force,
    `` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}^{2}}{{r}^{2}}``
    `` =14.4\,\mathrm{\,N\,}\times {10}^{-2}\,\mathrm{\,N\,}``
    `` =0.144\,\mathrm{\,N\,}`` (b) The components of the resultant force along it is zero because mg balances Tcosθ, as shown in the figure. So,
    F = Tsinθ (c) Tension in the string,
    Tsinθ = F ..(1)
    Tcosθ = mg ...(2)
    Squaring equations (1) and (2) and adding, we get
    `` {T}^{2}={F}^{2}+{\left(mg\right)}^{2}``
    `` ={\left(0.144\right)}^{2}+{\left(0.1\times 9.8\right)}^{2}``
    `` \Rightarrow T=0.986\,\mathrm{\,N\,}`` (d) --
    Page No 121:
  • #22-a
    the electric force on one of the charged balls
    Ans : By Coulomb's Law, the electric force,
    `` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}^{2}}{{r}^{2}}``
    `` =14.4\,\mathrm{\,N\,}\times {10}^{-2}\,\mathrm{\,N\,}``
    `` =0.144\,\mathrm{\,N\,}``
  • #22-b
    the components of the resultant force on it along and perpendicular to the string
    Ans : The components of the resultant force along it is zero because mg balances Tcosθ, as shown in the figure. So,
    F = Tsinθ
  • #22-c
    the tension in the string
    Ans : Tension in the string,
    Tsinθ = F ..(1)
    Tcosθ = mg ...(2)
    Squaring equations (1) and (2) and adding, we get
    `` {T}^{2}={F}^{2}+{\left(mg\right)}^{2}``
    `` ={\left(0.144\right)}^{2}+{\left(0.1\times 9.8\right)}^{2}``
    `` \Rightarrow T=0.986\,\mathrm{\,N\,}``
  • #22-d
    the acceleration of one of the balls.
    Answers are to be obtained only for the instant just after the release.
    Ans : --
    Page No 121: