NEET-XII-Physics
26: Laws of Thermodynamics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #5-aCalculate the work done by the gas.Ans : Work done on the gas = Pressure `` \times `` Change in volume of the system
Since pressure is also changing, we take the average of the given two pressures.
Now,
P = `` \left(\frac{1}{2}\right)\left(10+50\right)\times {10}^{3}``
= `` 30\times {10}^{3}`` Pa
Work done by the system of gas can be given by
`` 30\times {10}^{3}\times \left(50-200\right)\times {10}^{-6}``
`` =-4.5\,\mathrm{\,J\,}``
- #5-bIf no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?Ans : Since no heat is supplied to the system, ∆Q = 0.
Using the first law of thermodynamics, we get
∆U = - ∆W = 4.5 J
Page No 62:
- Qstn #6An ideal gas is taken from an initial state i to a final state f in such a way that the ratio of the pressure to the absolute temperature remains constant. What will be the work done by the gas?Ans : Let:
P1 = Initial pressure
P2 = Final pressure
T1 = Absolute initial temperature
T2 = Absolute final temperature
Given :
`` \frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}``
Using the ideal gas equation, we get
PV = nRT
If n is the number of moles of the gas and R is the universal gas constant, then
`` \frac{{P}_{1}}{{T}_{1}}\mathit{=}\frac{\mathit{n}\mathit{R}}{{\mathit{V}}_{\mathit{1}}}\,\mathrm{\,and\,}\frac{{P}_{2}}{{T}_{2}}\mathit{=}\frac{\mathit{n}\mathit{R}}{{\mathit{V}}_{\mathit{2}}}``
`` \Rightarrow {V}_{1}\mathit{=}{V}_{2}\left[\because \frac{{P}_{\mathit{1}}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}\right]``
`` ``
`` \mathit{\Rightarrow }\mathit{∆}V={V}_{2}\mathit{-}{V}_{1}=0``
`` ``
Thus, Work done by gas = P∆V = 0
Page No 62:
- Qstn #7Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.
FigureAns : Work done during any process, W = `` P∆V``
If both pressure and volume are changing during a process, then work done can be found out by finding the area under the PV diagram.
In path ACB, for line AC:
Since initial volume is equal to final volume, `` ∆V=0``.
`` \Rightarrow ``WAC = `` P∆V`` = 0
For line BC:
P = 30`` \times {10}^{3}`` Pa
`` {W}_{ACB}`` = WAC + WBC = 0 + P∆V
= 30 × 103 × (25 - 10) × 10-6
= 0.45 J
For path AB:
Since both pressure and volume are changing, we use the mean pressure to find the work done.
Mean pressure, P = `` \frac{1}{2}\times (30+10)\times {10}^{3}`` = 20 kPa
WAB = `` \frac{1}{2}`` × (10 + 30) × 103 × 15 × 10-6
= `` \frac{1}{2}`` × 40 × 15 × 10-3 = 0.30 J
Initial volume in path ADB, along line DB is the same as final volume. Thus, work done along this line is zero.
Along line AD, P = 10 kPa
W = WAD + WDB
= 10 × 103 (25 - 10) × 10-6 + 0
= 10 × 15 × 10-3 = 0.15 J
Page No 62:
- Qstn #8When a system is taken through the process abc shown in figure, 80 J of heat is absorbed by the system and 30 J of work is done by it. If the system does 10 J of work during the process adc, how much heat flows into it during the process?
FigureAns : Initial point is a and the final point is c.
As internal energy is a state function so it depends only on the initial and final points and not on the path followed by the system. This implies that change in internal energy for path abc and path adc is the same.
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
Here, ∆Q is the amount of heat absorbed and ∆U is the change in internal energy of the system. Also, ∆W is the work done by the system.
For path abc:
∆Q = 80 J, ∆W = 30 J
∆U = (80 - 30) J = 50 J
For path abc:
∆U =50 J (same as for path abc)
∆W = 10 J
∴ ∆Q = 10 J + 50 J = 60 J (∆U = 50 J)
Page No 63:
- Qstn #950 cal of heat should be supplied to take a system from the state A to the state B through the path ACB as shown in figure. Find the quantity of heat to be suppled to take it from A to B via ADB.
FigureAns : Given:
In path ACB,
∆Q = 50 cal = (50 × 4.2) J
∆Q = 210 J
∆W = WAC + WCB
Since initial and final volumes are the same along the line BC, change in volume of the system along BC is zero.
Hence, work done along this line will be zero.
For line AC:
P = 50 kPa
Volume changes from 200 cc to 400 cc.
`` \Rightarrow ∆V=400-200cc=200cc``
∆W = WAC + WCB
= 50 × 10-3 × 200 × 10-6 + 0
= 10 J
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
⇒ ∆U = ∆Q - ∆W = (210 - 10) J
∆U = 200 J
In path ADB, ∆Q = ?
∆U = 200 J (Internal energy depends only on the initial and final points and not on the path followed.)
⇒ ∆W = WAD + WDB = ∆W
Work done for line AD will also be zero.
For line DB:
P = 155 kPa
`` ∆V=400-200=200cc``
W = 0 + 155 × 103 × 200 × 10-6
W = 31 J
∆Q = ∆U + ∆W
∆Q= (200 + 31) J = 231 J
∆Q = 55 cal
Page No 63:
- Qstn #10Calculate the heat absorbed by a system in going through the cyclic process shown in figure.
FigureAns : Using the first law of thermodynamics, we get
`` ∆Q\mathit{=}\mathit{∆}U\mathit{+}\mathit{∆}W``
Since internal energy depends only on the initial and final points and for a cyclic process, initial and final points are the same, change in internal energy of the system during this process will be zero.
`` \Rightarrow ∆U=0``
`` \Rightarrow ∆Q=∆W``
Heat absorbed = Work done
Work done = Area under the graph in the given case
Thus,
Heat absorbed = Area of the circle
Diameter of the circle = 300 `` -`` 100 = 200
Heat absorbed = `` \pi ``× 104 × 10-6 × 103 J
= 3.14 × 10 = 31.4 J
Page No 63:
- Qstn #11A gas is taken through a cyclic process ABCA as shown in figure. If 2.4 cal of heat is given in the process, what is the value of J ?
FigureAns : Heat given in the process, ∆Q = 2.4 cal
∆W = WAB + WBC + WCA
For line AB:
Change in volume, `` ∆V=0``
`` \therefore {W}_{\,\mathrm{\,AB\,}}=0``
For line BC:
`` \,\mathrm{\,Mean\,}\,\mathrm{\,pressure\,},P=\frac{1}{2}\times (100+200)\,\mathrm{\,kPa\,}=150\times {10}^{3}\,\mathrm{\,Pa\,}``
`` ∆V=(700-500)\,\mathrm{\,cc\,}=200\,\mathrm{\,cc\,}``
`` {W}_{\,\mathrm{\,BC\,}}=150\times {10}^{3}\times 200\times {10}^{-6}``
`` {W}_{\,\mathrm{\,BC\,}}=30\,\mathrm{\,J\,}``
For line AC:
P = 100 kPa
`` ∆V=200cc``
WCA = 100 × 103 × 200 × 10-6
Total work done in the one cycle is given by
∆W = 0 + 150× 103 × 200 × 10-6 - 100 × 103 × 200 × 10-6
∆W = `` \frac{1}{2}`` × 300 × 103 × 200 × 10-6 - 20
∆W = 30 J - 20 J = 10 J
∆U = 0 (in a cyclic process)
∆Q = ∆U + ∆W
⇒ 2.4J = 10
`` \Rightarrow J=\frac{10}{2.4}=\frac{100}{24}=\frac{25}{6}=4.17\,\mathrm{\,J\,}/\,\mathrm{\,cal\,}``
Page No 63:
- Qstn #12A substance is taken through the process abc as shown in figure. If the internal energy of the substance increases by 5000 J and a heat of 2625 cal is given to the system, calculate the value of J.
FigureAns : Given:
Heat given to the system, ∆Q = 2625 cal
Increase in the internal energy of the system, ∆U = 5000 J
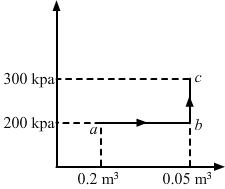
From the graph, we get
W = Area of the rectangle formed under line ab + Area under line bc
For line BC:
Change in volume = 0
`` {W}_{BC}=P∆V=0``
∆W = Area of the rectangle
∆W = 200 × 103 × 0.03
= 6000 J
We know,
∆Q = ∆W + ∆U
⇒ 2625 cal = 6000 J + 5000 J
`` \Rightarrow J=\frac{11000}{2625}=4.19\,\mathrm{\,J\,}/\,\mathrm{\,cal\,}``
Page No 63:
- Qstn #13A gas is taken along the path AB as shown in figure. If 70 cal of heat is extracted from the gas in the process, calculate the change in the internal energy of the system.
FigureAns : Given: 70 cal of heat is extracted from the system.
Here,
∆Q = `` -``70 cal = `` -``(70 × 4.2) J = `` -``294 J
From the first law of thermodynamics, we get
∆W = P`` ∆V``
If P is the average pressure between points A and B and `` ∆V`` is the change in volume of the system while going from point A to B, then
∆W = `` -```` \frac{1}{2}`` × (200 + 500) × 103 × (150 × 10-6)
∆W = `` -```` \frac{1}{2}`` × 700 × 150 × 10-3
∆W = `` -``525 × 10-1 = `` -``52.5 J
Here, negative sign is taken because the final volume is less than the initial volume.
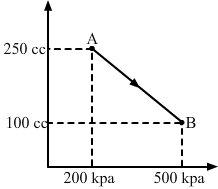
∆U = ?
∆Q = ∆U + ∆W
∆Q = `` -``294 J
Here, negative sign indicates that heat is extracted out from the system.
⇒ - 294 = ∆U `` -`` 52.5
⇒ ∆U = - 294 + 52.5 = `` -`` 241.5 J
Page No 63:
- Qstn #14The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3 against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.Ans : Let change in volume of the gas be ∆V.
∆V = (200 - 100) cm3 = 100 cm3
= 10-4 m3
p = 1 × 105 Pa
Change in internal energy of the system, ∆U = 1.5 pV
∆U = 1.5 × 105 × 10-4 = 15 J
∆W = p∆V
= 105 × 10-4 = 10 J
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W = 10 + 15 = 25 J
Thus, heat absorbed by the system is 25 J.
Page No 63:
- Qstn #15A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.Ans : Given: Heat supplied to the system, ∆Q = 10 J
Change in volume of the system, ∆V = Area of cross section × Displacement of the piston
= A × 10 cm
= (4 × 10) cm3 = 40 × 10-6 m3
P = 100 kPa
∆W = P∆V = 100 × 103 × 40 × 10-6 m3
= 4 J
∆U = ?
Using the first law of thermodynamics, we get
10 = ∆U + ∆W
⇒ 10 = ∆U + 4
⇒ ∆U = 6 J
Here, positive sign indicates that the internal energy of the system has increased.
Page No 63:
- Qstn #16A gas is initially at a pressure of 100 kPa and its volume is 2.0 m3. Its pressure is kept constant and the volume is changed from 2.0 m3 to 2.5 m3. Its Volume is now kept constant and the pressure is increased from 100 kPa to 200 kPa. The gas is brought back to its initial state, the pressure varying linearly with its volume.
- #16-aWhether the heat is supplied to or extracted from the gas in the complete cycle?Ans : Given:
P1 = 100 kPa,
V1 = 2 m3
`` {V}_{2}`` = 2.5 m3
∆V = 0.5 m3
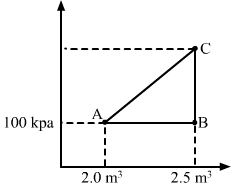
Work done, W = P∆V
`` W=100\times {10}^{3}\times 0.5``
`` W=5\times {10}^{4}\,\mathrm{\,J\,}``
WAB = Area under line AB = 5`` \times ``104 J
If volume is kept constant for line BC, then ∆V = 0.
WBC = P∆V = 0
Work done while going from point B to C = 0
When the system comes back to the initial point A from C, work done is equal to area under line AC.
WCA = Area of triangle ABC + Area of rectangle under line AB
Total work done, W = Area enclosed by the ABCA
W = WAC `` -``WAB
From the graph, we see that the area under AC is greater than the area under AB. We also see that heat is extracted from the system as change in the internal energy is zero.
- #16-bHow much heat was supplied or extracted?Ans : Amount of heat extracted = Area enclosed under ABCA
`` =\frac{1}{2}\times 0.5\times 100\times {10}^{3}=25000\,\mathrm{\,J\,}``
Page No 63: