26: Laws Of Thermodynamics : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

26: Laws of Thermodynamics

with Solutions - page 5

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #17
Consider the cyclic process ABCA, shown in figure, performed on a sample of 2.0 mol of an ideal gas. A total of 1200 J of heat is withdrawn from the sample in the process. Find the work done by the gas during the part BC.
Figure
Ans : Given:
Number of moles of the gas, n = 2
∆Q = - 1200 J (Negative sign shows that heat is extracted out from the system)
∆U = 0 (During cyclic process)

Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
⇒ -1200 = 0 + (W_AB + W_BC + W_CA)
Since the change in volume of the system applies on line CA, work done during CA will be zero.
From the ideal gas equation, we get
PV = nRT
P∆V = nR∆T
W = P∆V = nR∆T
⇒ ∆Q = ∆U + ∆W
⇒ -1200 = nR∆T + W_BC + 0
⇒ -1200 = 2 × 8.3 × 200 + W_BC
W_BC = - 400 × 8.3 - 1200
= - 4520 J
Page No 63:

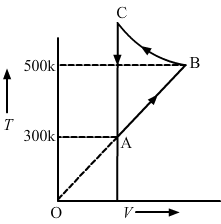
Qstn #18
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Figure
Ans : Given: Number of moles of the gas, n = 2 moles
The system's volume is constant for lines bc and da. Therefore,
∆V = 0
Thus, work done for paths da and bc is zero.
`` \Rightarrow {W}_{da}={W}_{bc}=0``
Since the process is cyclic, ∆U is equal to zero.
Using the first law, we get
∆W = ∆Q
∆W = ∆W_AB + ∆W_CD
Since the temperature is kept constant during lines ab and cd, these are isothermal expansions.
Work done during an isothermal process is given by
W = nRT`` \,\mathrm{\,ln\,}\frac{{V}_{f}}{{V}_{i}}``
If `` {V}_{f}\,\mathrm{\,and\,}{V}_{i}`` are the initial and final volumes during the isothermal process, then
`` W=n{\,\mathrm{\,RT\,}}_{1}ln\left(\frac{2{\,\mathrm{\,V\,}}_{0}}{{\,\mathrm{\,V\,}}_{0}}\right)+n{\,\mathrm{\,RT\,}}_{2}ln\left(\frac{{\,\mathrm{\,V\,}}_{0}}{2{\,\mathrm{\,V\,}}_{0}}\right)``
W = nR × 2.303 × log 2 × (500 - 300)
W = 2 × 8.314 × 2.303 × 0.301 × 200
W = 2305.31 J
Page No 63:

Qstn #19
Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg^-1 K^-1 and its densities at 0°C and 4°C are 999.9 kg m^-3 and 1000 kg m^-3 respectively. Atmospheric pressure = 10⁵ Pa.
Ans : Given:
Mass of water, M = 2 kg
Change in temperature of the system, ∆θ = 4°C = 277 K
Specific heat of water, s_w = 4200 J/kg-°C
Initial density, p₀ = 999.9 kg/m³
Final density, p_f = 1000 kg/m³
P = 10⁵ Pa
Let change in internal energy be ∆U.
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
Also, ∆Q = ms∆θ
W = P∆V = P(`` {V}_{f}-{V}_{i}``)
⇒ ms∆θ = ∆U + P (V₀- V₄)
⇒ 2 × 4200 × 4= ∆U + 10⁵ (∆V)
⇒ 33600 = ∆U + 10⁵ `` \left(\frac{m}{{p}_{0}}-\frac{m}{{p}_{f}}\right)``
⇒ 33600 = ∆U + 10⁵ × (`` -``0.0000002)
⇒ 33600 = ∆U `` -`` 0.02
∆U = (33600 `` -`` 0.02) J
Page No 63:

Qstn #20
Calculate the increase in the internal energy of 10 g of water when it is heated from 0°C to 100°C and converted into steam at 100 kPa. The density of steam = 0.6 kg m^-3. Specific heat capacity of water = 4200 J kg^-1 °C^-1 and the latent heat of vaporization of water = 2.25 × 10 6J kg^-1.
Ans : Given:
Mass of water, m = 10 g = 0.01 kg
Pressure, P = 10⁵ Pa
Specific heat capacity of water, c = 1000 J/Kg `` °C``
Latent heat, L = 2.25`` \times {10}^{6}\,\mathrm{\,J\,}/\,\mathrm{\,Kg\,}``
`` ∆t=\,\mathrm{\,Change\,}\,\mathrm{\,in\,}\,\mathrm{\,temperature\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,system\,}=100°\,\mathrm{\,C\,}=373\,\mathrm{\,K\,}``
∆Q = Heat absorbed to raise the temperature of water from 0`` °\,\mathrm{\,C\,}\,\mathrm{\,to\,}100°\,\mathrm{\,C\,}`` + Latent heat for conversion of water to steam
∆Q = `` mc∆t+mL``
= 0.01 × 4200 × 100 + 0.01 × 2.5 × 10⁶
= 4200 + 25000 = 29200 J
∆W = P∆V
∆V`` =\,\mathrm{\,mass\,}\left(\frac{1}{\,\mathrm{\,final\,}\,\mathrm{\,density\,}}-\frac{1}{\,\mathrm{\,initial\,}\,\mathrm{\,density\,}}\right)``
`` ∆\,\mathrm{\,V\,}=\left(\frac{0.01}{0.6}\right)-\left(\frac{0.01}{1000}\right)=0.01699``
∆W = P∆V = 0.01699 × 10⁵ = 1699 J
Using the first law, we get
∆Q = ∆W + ∆U
∆U = ∆Q - ∆W = 29200 - 1699
= 27501 = 2.75 × 10⁴ J
Page No 64:

Qstn #21
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p₁, T₁ on the left and p₂, T₂ on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides.
Ans :

Let n₁ , U₁ and n₂ ,U₂ be the no. of moles , internal energy of ideal gas in the left chamber and right chamber respectively.

#21-a
How much work has been done by the gas on the left part?
Ans :
As the diathermic wall is fixed, so final volume of the chambers will be same. Thus, ΔV = 0, hence work done ΔW= PΔV = 0

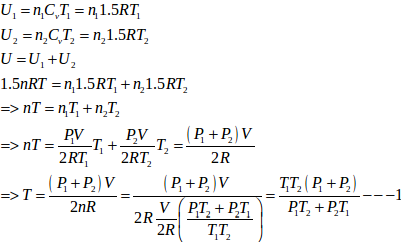
#21-b
Find the final pressures on the two sides.
Ans : Let final pressure in the first and second compartment P₁’ and P₂’.

#21-c
Find the final equilibrium temperature.
Ans :

#21-d
How much heat has flown from the gas on the right to the gas on the left?
Figure
Ans :
Page No 64:

Qstn #22
An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find

#22-a
the work done by the gas in the left part during the process,
Ans : Since the conducting wall is fixed, the work done by the gas on the left part during the process is zero because the change in volume will be zero due to the fixed position of the wall.

#22-b
the temperature on the two sides in the beginning,
Ans : For left side:
Let the initial pressure on both sides of the wall be p.
We know,
Volume =`` \frac{\mathit{V}}{\mathit{2}}``
Number of moles, n = 1
Let initial temperature be T₁.
Using the ideal gas equation, we get
`` \frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}nR{T}_{\mathit{1}}``
`` \mathit{\Rightarrow }\frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}\mathit{\left(}\mathit{1}\mathit{\right)}RT``
`` \mathit{\Rightarrow }{T}_{\mathit{1}}\mathit{=}\frac{\mathit{P}\mathit{V}}{\mathit{(}\mathit{2}\mathit{m}\mathit{o}\mathit{l}\mathit{e}\mathit{s}\mathit{)}\mathit{R}}``
For right side:
Number of moles, n = 2
Let the initial temperature be T₂.
We know,
Volume =`` \frac{\mathit{V}}{\mathit{2}}``
`` \frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}nR{T}_{\mathit{2}}``
`` \mathit{\Rightarrow }{T}_{\mathit{2}}\mathit{=}\frac{\mathit{P}\mathit{V}}{\mathit{(}\mathit{4}\mathit{m}\mathit{o}\mathit{l}\mathit{e}\mathit{s}\mathit{)}\mathit{R}}``

#22-c
the final common temperature reached by the gases,
Ans :

Here,

U = 1.5nRT

T = temperature at the equilibrium

P₁ = P₂ = P

n₁ = 1 mol

n₂ = 2 mol

Let T₁ and T₂ be the initial temperatures of the left and right chamber respectively.

Applying eqn. of state

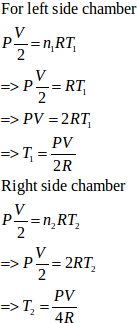
We know that total n = n₁ + n₂ = 3

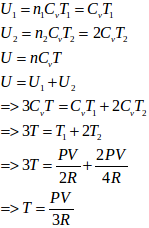
#22-d
the heat given to the gas in the right part and
(d) the increase in the internal energy of the gas in the left part.
Ans : For RHS:
∆Q = ∆U as ∆W = 0
∆U = 1.5 n₂R (T - T₂)
When T is the final temperature and T₂ is the initial temperature of side 1, we get
= 1.5 × 2 × R (T - T₂)
= 1.5 × 2 × `` \frac{4\,\mathrm{\,PV\,}-3\,\mathrm{\,PV\,}}{4\times 3\,\mathrm{\,mole\,}}``
`` ``
`` =\frac{3\times \,\mathrm{\,PV\,}}{4\times 3\,\mathrm{\,mole\,}}=\frac{\,\mathrm{\,PV\,}}{4}``
(d) If dW = 0, then using the first law, we get
dQ = - dU
⇒ dU = - dQ = `` \frac{-\,\mathrm{\,PV\,}}{4}``