NEET-XII-Physics
24: Kinetic Theory of Gases
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #16Find the average magnitude of linear momentum of a helium molecule in a sample of helium gas at 0°C. Mass of a helium molecule = 6.64 × 10-27 kg and Boltzmann constant = 1.38 × 10-23 J K-1.Ans : Here,
​m = 6.64 × 10-27 kg
T = 273 K
`` \,\mathrm{\,Average\,}\,\mathrm{\,speed\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,He\,}\,\mathrm{\,atom\,}\,\mathrm{\,is\,}\,\mathrm{\,given\,}\,\mathrm{\,by\,}``
`` {\,\mathrm{\,V\,}}_{\,\mathrm{\,avg\,}}=\sqrt{\frac{8kT}{\pi m}}``
`` =\sqrt{\frac{8\times 1.38\times {10}^{-23}\times 273}{3.14\times 6.64\times {10}^{-27}}}``
`` =1202.31``
`` ``
We know,
Momentum = m × Vavg
= 6.64 × 10-27 × 1201.35
= 7.97 × 10-24
= 8 × 10-24 kg-m/s
- Qstn #17The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.Ans : Mean velocity is given by
`` {V}_{avg}=\sqrt{\frac{8RT}{\pi M}}``
Let temperature for H and He respectively be T​1 and T2, respectively.
For hydrogen:
MH = 2g = 2`` \times ``10-3 kg
For helium:
MHe= 4 g = 4`` \times ``10-3 kg
Now,
A/q`` \sqrt{\frac{8R{T}_{1}}{\pi {M}_{H}}}=\sqrt{\frac{8R{T}_{2}}{\pi {M}_{He}}}``
`` \Rightarrow \sqrt{\frac{8R{T}_{1}}{2\times {10}^{-3}\pi }}=\sqrt{\frac{8R{T}_{2}}{\pi \times 4\times {10}^{-3}}}``
`` \Rightarrow \sqrt{\frac{{T}_{1}}{2}}=\sqrt{\frac{{T}_{2}}{4}}``
`` \Rightarrow \frac{{T}_{1}}{{T}_{2}}=\frac{1}{2}``
`` \Rightarrow {T}_{1}:{T}_{2}=1:2``
- Qstn #18At what temperature the mean speed of the molecules of hydrogen gas equals the escape speed from the earth?Ans : Mean speed of the molecule is given by
`` \sqrt{\frac{8\,\mathrm{\,RT\,}}{\,\mathrm{\,\pi M\,}}}``
`` \,\mathrm{\,For\,}\,\mathrm{\,H\,}\,\mathrm{\,molecule\,},M=2\times {10}^{-3}kg``
`` =\sqrt{\frac{4\,\mathrm{\,RT\,}\times {10}^{3}}{\pi }}``
For escape velocity of Earth:
`` \,\mathrm{\,Suppose\,}r\,\mathrm{\,be\,}\,\mathrm{\,the\,}\,\mathrm{\,radius\,}\,\mathrm{\,of\,}\,\mathrm{\,Earth\,}.``
`` v=\sqrt{\frac{2GM}{r}}``
`` \,\mathrm{\,Multiplying\,}\,\mathrm{\,neumerator\,}\,\mathrm{\,and\,}\,\mathrm{\,denominator\,}\,\mathrm{\,by\,}\,\mathrm{\,R\,},\,\mathrm{\,we\,}\,\mathrm{\,get\,}``
`` {v}_{c}=\sqrt{\frac{GM}{{r}^{2}}2r}``
`` g=\frac{GM}{{r}^{2}}``
`` {v}_{c}=\sqrt{2gr}``
`` \sqrt{\frac{4\,\mathrm{\,RT\,}\times {10}^{3}}{\pi }}=\sqrt{2gr}``
`` \Rightarrow \frac{2\times 8.314\times T\times {10}^{3}}{3.142}=9.8\times 6.37\times {10}^{6}``
`` \Rightarrow T\approx 11800K``
Page No 35:
- Qstn #19Find the ratio of the mean speed of hydrogen molecules to the mean speed of nitrogen molecules in a sample containing a mixture of the two gases.Ans : We know,
`` {V}_{avg}=\sqrt{\frac{8RT}{\pi M}}``
Molar mass of H2 = MH = 2`` \times ``10-3 kg
Molar mass of N2 = MN = 28`` \times ``10-3 kg
Now,
`` <V{>}_{H}=\sqrt{\frac{8RT}{\pi {M}_{H}}}``
`` <V{>}_{N}=\sqrt{\frac{8RT}{\pi {M}_{N}}}``
`` \frac{<V{>}_{H}}{<V{>}_{N}}=\sqrt{\frac{{M}_{N}}{{M}_{H}}}=\sqrt{\frac{28}{2}}=\sqrt{14}=3.74``
Page No 35:
- Qstn #20Figure shows a vessel partitioned by a fixed diathermic separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part equals the mean speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in the right part.
Figure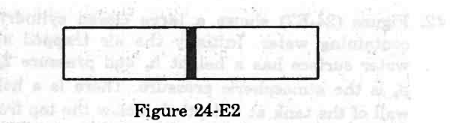
Ans : Let the temperature of gas in both the chambers be T.
Let the molar mass of gas in the left chamber and right chamber be M​1 and M2, respectively.
Let mass of gas in the left and right chamber be m1 and m2, respectively. Then,
`` A/Q``
`` {v}_{rms}=\sqrt{\frac{3kT}{{m}_{1}}}=\sqrt{\frac{8kT}{\,\mathrm{\,\pi \,}{m}_{2}}}``
`` \Rightarrow 3{m}_{1}=\frac{8{m}_{2}}{3.14}``
`` ``
`` \Rightarrow \frac{{m}_{2}}{{m}_{1}}=1.18``
Page No 35:
- Qstn #21Estimate the number of collisions per second suffered by a molecule in a sample of hydrogen at STP. The mean free path (average distance covered by a molecule between successive collisions) = 1.38 × 10-5 cm.Ans : Here,
`` \lambda =1.38\times {10}^{-8}\,\mathrm{\,m\,}``
`` ``
T = 273 K
M = `` 2\times {10}^{-3}\,\mathrm{\,kg\,}``
Average speed of the H molecules is given by
`` {v}_{avg}=\sqrt{\frac{8RT}{\,\mathrm{\,\pi M\,}}}``
`` =\sqrt{\frac{8\times 8.31\times 273}{3.14\times 2\times {10}^{-3}}}``
`` =1700m{s}^{-1}``
`` ``
`` ``
`` ``
The time between two collisions is given by
`` t=\frac{\lambda }{{v}_{avg}}``
`` \Rightarrow t=\frac{1.38\times {10}^{-8}}{1700}``
`` \Rightarrow t=8\times {10}^{-12}s``
`` \,\mathrm{\,Number\,}\,\mathrm{\,of\,}\,\mathrm{\,collisions\,}\,\mathrm{\,in\,}1\,\mathrm{\,s\,}=\frac{1}{8.11\times {10}^{-12}}=1.23\times {10}^{11}``
Page No 35:
- Qstn #22Hydrogen gas is contained in a closed vessel at 1 atm (100 kPa) and 300 K.Ans : Here,
P = 105 Pa
T = 300 K
For H2
M = 2×10-3 kg
- #22-aCalculate the mean speed of the molecules.Ans : `` \begin{array}{l}\left(\text{a}\right)\text{Mean speed is given by}\\ <v>=\sqrt{\frac{8RT}{\pi M}}\\ =\sqrt{\frac{8\times 8.3\times 300\times 7}{2\times {10}^{-3}\times 22}}\\ =1780{\text{ms}}^{-1}\\
- #22-bSuppose the molecules strike the wall with this speed making an average angle of 45° with it. How many molecules strike each square metre of the wall per second?Ans : {\text{Let us consider a cubic volume of 1 m}}^{3}.\\ V=1{\text{m}}^{3}\\ \text{Momentum of 1 molecule normal to the striking surface before collision =}mu\,\mathrm{\,sin\,}{45}^{0}\\ \text{Momentum of 1 molecule normal to the striking surface after collision =}-mu\,\mathrm{\,sin\,}{45}^{0}\\ \text{Change in momentum of the molecule =}2mu\,\mathrm{\,sin\,}{45}^{0}=\sqrt{2}mu\\ \text{Change in momentum of n molecules =}2mnu\,\mathrm{\,sin\,}{45}^{0}=\sqrt{2}mnu\\ \text{Let}\Delta \text{t be the time taken in changing the momentum.}\\ \text{Force per unit area due to one molecule =}\frac{\sqrt{2}mu}{\Delta t}=\frac{\sqrt{2}mu}{\Delta t}\\ \text{Observed pressure due to collision by n molecules =}\frac{\sqrt{2}mnu}{\Delta t}={10}^{5}\\ n=\raisebox{1ex}{$\frac{\sqrt{2}mnu}{\Delta t}$}\!\left/ \!\raisebox{-1ex}{$\frac{\sqrt{2}mu}{\Delta t}$}\right.=\frac{{10}^{5}}{\sqrt{2}mu}\\ 6.0\times {10}^{23}\text{molecules}=\text{2}\times {\text{10}}^{-3}\text{kg}\\ \text{1 molecule =}\frac{\text{2}\times {\text{10}}^{-3}}{6\times {10}^{23}}=3.3\times {10}^{-27}\text{kg}\\ \Rightarrow n=\frac{{10}^{5}}{\sqrt{2}\times 3.3\times {10}^{-27}\times 1780}=1.2\times {10}^{28}\end{array}``
Page No 35:
- Qstn #23Air is pumped into an automobile tyre’s tube up to a pressure of 200 kPa in the morning when the air temperature is 20°C. During the day the temperature rises to 40°C and the tube expands by 2%. Calculate the pressure of the air in the tube at this temperature.Ans : `` \begin{array}{l}\text{Here,}\\ {P}_{1}=2\times {10}^{5}\,\mathrm{\,Pa\,}\\ {P}_{2}=?\\ {T}_{1}=293K\\ {T}_{2}=313K\\ {V}_{2}={V}_{1}+0.02{V}_{1}={V}_{1}\left(1.02\right)\\ \text{Now,}\\ \frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{2}{V}_{2}}{{T}_{2}}\\ \Rightarrow \frac{2\times {10}^{5}{V}_{1}}{293}=\frac{{P}_{2}{V}_{1}\left(1.02\right)}{313}\\ \Rightarrow {P}_{2}=\frac{2\times {10}^{5}\times 313}{293\times 1.02}=209\text{kPa}\end{array}``
Page No 35:
- Qstn #24Oxygen is filled in a closed metal jar of volume 1.0 × 10-3 m3 at a pressure of 1.5 × 105 Pa and temperature 400 K. The jar has a small leak in it. The atmospheric pressure is 1.0 × 105 Pa and the atmospheric temperature is 300 K. Find the mass of the gas that leaks out by the time the pressure and the temperature inside the jar equalise with the surrounding.Ans : `` \begin{array}{l}\text{Here,}\\ {V}_{1}=1.0\times {10}^{-3}{m}^{3}\\ {T}_{1}=400K\\ {P}_{1}=1.5\times {10}^{5}Pa\\ {P}_{2}=1.0\times {10}^{5}Pa\\ {T}_{2}=300\\ M=32g\\ \text{Number of moles in the jar before}{n}_{1}\text{=}\frac{{P}_{1}{V}_{1}}{R{T}_{1}}\\ \text{Volume of the gas when pressure becomes equal to external pressure is given by}\\ \frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{2}{V}_{2}}{{T}_{2}}\\ \Rightarrow {V}_{2}=\frac{{P}_{1}{V}_{1}{T}_{2}}{{P}_{2}{T}_{1}}\\ \Rightarrow {V}_{2}=\frac{1.5\times {10}^{5}\times 1.0\times {10}^{-3}\times 300}{1.0\times {10}^{5}\times 400}=1.125\times {10}^{-3}\\ \text{Net volume of leaked gas =}{V}_{2}-{V}_{1}\\ =1.125\times {10}^{-3}-1.0\times {10}^{-3}\\ =1.25\times {10}^{-4}{\text{m}}^{3}\\ {\text{Let n}}_{2}\text{be the number of moles of leaked gas.}\,\mathrm{\,Applying\; equation\; of\; state\; on\; this\; amount\; of\; gas,\,}\,\mathrm{\,we\,}\,\mathrm{\,get\,}\\ \\ {n}_{2}=\frac{{P}_{2}{V}_{2}}{R{T}_{2}}=\frac{1.0\times {10}^{5}\times 1.25\times {10}^{-4}}{8.3\times 300}=0.005\\ \text{Mass of leaked gas= 32}\times \text{0}\text{.005=0}\text{.16 g}\end{array}``
Page No 35:
- Qstn #25An air bubble of radius 2.0 mm is formed at the bottom of a 3.3 m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure = 1.0 × 105 Pa and density of water = 1000 kg m-3.Ans : `` \begin{array}{l}\text{Here,}\\ {\text{V}}_{1}=\frac{4}{3}\pi {(2.0\times {10}^{-3})}^{3}\\ h=3.3\text{m}\\ {P}_{1}={P}_{o}+\rho gh\\ \Rightarrow {P}_{1}=1.0\times {10}^{5}+1000\times 9.8\times 3.3\\ \Rightarrow {P}_{1}=1.32\times {10}^{5}Pa\\ {P}_{2}=1.0\times {10}^{5}Pa\\ \text{Since temperature remains the same, applying Boyle's law we get}\\ {P}_{1}{V}_{1}={P}_{2}{V}_{2}\\ \Rightarrow {V}_{2}=\frac{{P}_{1}{V}_{1}}{{P}_{2}}\\ \Rightarrow {V}_{2}=\frac{1.32\times {10}^{5}\times \frac{4}{3}\pi {(2.0\times {10}^{-3})}^{3}}{1.0\times {10}^{5}}\\ {\text{Let R}}_{2}\text{be the new radius. Then,}\\ \frac{4}{3}\pi {R}_{2}^{3}=\frac{1.32\times {10}^{5}\times \frac{4}{3}\pi {(2.0\times {10}^{-3})}^{3}}{1.0\times {10}^{5}}\\ \Rightarrow {R}_{2}^{3}=\frac{1.32\times {10}^{5}\times {(2.0\times {10}^{-3})}^{3}}{1.0\times {10}^{5}}\\ \Rightarrow {R}_{3}=\sqrt[3]{\frac{1.32\times {10}^{5}\times {(2.0\times {10}^{-3})}^{3}}{1.0\times {10}^{5}}}\\ \Rightarrow {R}_{3}=2.2\times {10}^{-3}m\end{array}``
Page No 35:
- Qstn #26Air is pumped into the tubes of a cycle rickshaw at a pressure of 2 atm. The volume of each tube at this pressure is 0.002 m3. One of the tubes gets punctured and the volume of the tube reduces to 0.0005 m3. How many moles of air have leaked out? Assume that the temperature remains constant at 300 K and that the air behaves as an ideal gas.Ans : `` \begin{array}{l}\text{Here,}\\ {P}_{1}=2\times {10}^{5}pa\\ {V}_{1}=0.002{\text{m}}^{\text{3}}\\ {V}_{2}=0.0005{m}^{3}\\ {T}_{1}={T}_{2}=300K\\ \\ \,\mathrm{\,Number\; of\; moles\; initially\,},{n}_{1}=\frac{{P}_{1}{V}_{1}}{R{T}_{1}}\\ \Rightarrow {n}_{1}=\frac{2\times {10}^{5}\times 0.002}{8.3\times 300}\\ \Rightarrow {n}_{1}=0.16\\ \text{Applying equation of state, we get}\\ {P}_{2}{V}_{2}={n}_{2}RT\\ \text{Assuming the final pressure becomes equal to the atmospheric pressure, we get}\\ {P}_{2}=1.0\times {10}^{5}pa\\ \Rightarrow {n}_{2}=\frac{{P}_{2}{V}_{2}}{RT}\\ \Rightarrow {n}_{2}=\frac{1.0\times {10}^{5}\times 0.0005}{8.3\times 300}\\ \Rightarrow {n}_{2}=0.02\\ \text{Number of leaked moles =}{n}_{2}-{n}_{1}\\ =0.16-0.02\\ =0.14\end{array}``
Page No 35:
- Qstn #270.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.Ans : `` \begin{array}{l}\text{Here,}\\ m=0.040g\\ M=4g\\ n=\frac{0.040}{4}=0.01\\ {T}_{1}=\left(100+273\right)K=373K\\ \text{He is a monoatomic gas. Thus,}\\ {C}_{v}=3\times \left(\frac{1}{2}R\right)\\ \Rightarrow {C}_{v}=1.5\times 8.3=12.45\\ {\text{Let the initial internal energy be U}}_{1}\text{.}\\ {\text{Let the final internal energy be U}}_{2}\text{.}\\ {U}_{2}-{U}_{1}=n{C}_{v}({T}_{2}-{T}_{1})\\ \Rightarrow 0.01\times 12.45({T}_{2}-373)=12\\ \Rightarrow {T}_{2}=469K\\ {\text{The temperature in}}^{0}C\text{can be obtained as follows:}\end{array}``
`` {\,\mathrm{\,469\; -\; 273\; =\; 196\,}}^{0}C``
`` ``
`` ``
Page No 35:
- Qstn #28During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.Ans : `` \begin{array}{l}\text{Applying equation of state of an ideal gas, we get}\\ PV=nRT\\ \Rightarrow P=\frac{nRT}{V}...1\\ \text{Taking differentials, we get}\\ \Rightarrow PdV+VdP=nRdT...2\\ \text{Applying the additional law, we get}\\ P{V}^{2}=c\\ {V}^{2}dP+2VPdV=0\\ \Rightarrow VdP+2PdV=0...3\\ \text{Subtracting eq.}\left(\text{3}\right)\text{from eq.}\left(\text{2}\right)\text{, we get}\\ PdV=-nRdT\\ \Rightarrow dV=-\frac{nR}{P}dT\\ \text{Now,}\\ \text{⇒}dV=-\frac{V}{T}dT\left[\,\mathrm{\,From\,}\,\mathrm{\,eq\,}.\left(1\right)\right]\\ \Rightarrow \frac{dV}{V}=-\frac{dT}{T}\\ {\text{Integrating between T}}_{2}{\text{and T}}_{1}\text{, we get}\\ \Rightarrow \underset{{V}_{1}}{\overset{2V}{\int }}=-\underset{{T}_{1}}{\overset{{T}_{2}}{\int }}\\ \Rightarrow \,\mathrm{\,ln\,}\left(2V\right)-ln\left(V\right)=\,\mathrm{\,ln\,}\left({T}_{1}\right)-\,\mathrm{\,ln\,}\left({T}_{2}\right)\\ \Rightarrow \,\mathrm{\,ln\,}\left(\frac{2V}{V}\right)=\,\mathrm{\,ln\,}\left(\frac{{T}_{1}}{{T}_{2}}\right)\\ \Rightarrow {T}_{2}=\frac{{T}_{1}}{2}\end{array}``
Page No 35: