HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

neet 2020 questions with solutions year:2020

with Solutions -

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #1
    For which one of the following, Bohr model is not valid?
    (A)Hydrogen atom
    (B)Singly ionised helium atom `` (He^+) ``
    (C)Deuteron atom
    (D)Singly ionised neon atom `` (Ne^+) ``
    digAnsr:   D
    Ans : Bohr model is applicable for only single electron species. Singly ionised neon atom has more than one electron in orbit. Hence, Bohr model is not valid
  • Qstn #2
    The ratio of contributions made by the electric field and magnetic field components to the intensity of an electromagnetic wave is : (c = speed of electromagnetic waves)
    (A)c : 1
    (B)1 : 1
    (C)1 : c
    (D) `` 1 : c^2 ``
    digAnsr:   B
    Ans : In an electromagnetic wave, half of the intensity is provided by the electric field and half by the magnetic field. Hence, required ratio should be `` 1 : 1 ``
  • Qstn #3
    The Brewsters angle `` i_b `` for an interface should be:
    (A) `` 0°< i b < 30° ``
    (B) `` 30°< i_b < 45° ``
    (C) `` 45°< i_b < 90° ``
    (D) `` i_b = 90° ``
    digAnsr:   C
    Ans : `` \mu=tan\,i_{b} ``
    `` 1<\,\mu<\,\infty ``
    `` 1<\,tan\,i_{b}<\,\infty ``
    `` tan^{-1}\left(1\right)<\,i_{b}<\,tan^{-1}\left(\infty\right) ``
    `` 45^{\circ}<\,i_{b}<\,90^{\circ} ``
  • Qstn #4
    A cylinder contains hydrogen gas at pressure of 249 kPa and temperature `` 27^\circ\,C `` . Its density is : `` (R = 8.3\,J\,mol^{-1}K^{-1} `` )
    (A) `` 0.5 \,kg/m^3 ``
    (B) `` 0.2 \,kg/m^3 ``
    (C) `` 0.1 \,kg/m^3 ``
    (D) `` 0.02 \,kg/m^3 ``
    digAnsr:   B
    Ans : We can express, an ideal gas equation as
    `` \frac{P}{\rho}=\frac{R.T}{Mw} ``
    `` \Rightarrow \rho=\frac{pMw}{RT} ``
    `` =\frac{249 \times 10^{3}\times 2 \times 10^{-3}}{8.314 \times 300} ``
    `` =0.199 ``
    `` \Rightarrow \rho=0.2 kg/m^{3} ``
  • Qstn #5
    A ray is incident at an angle of incidence `` i `` on one surface of a small angle prism(with angle of prism A) and emerges normally from the opposite surface. If the refractive index of the material of the prism is `` \mu `` . then the angle of incidence is nearly equal to:
    (A) `` \frac {A}{2\mu} ``
    (B) `` \frac {2A}{\mu} ``
    (C) `` \mu A ``
    (D) `` \frac {\mu \,A}{2} ``
    digAnsr:   C
    Ans : Light ray emerges from another surface normally, hence e(angle of emergence) = 0
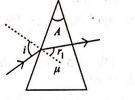
    image
    `` \Rightarrow r_{2}=0 ``
    `` r_{1}+r_{2}=A ``
    `` \Rightarrow r_{1}=A ``
    Applying Snell’s law on first surface,
    `` 1. sin\,i=\mu\,sin\,r_{1} ``
    For small angle , `` sin\,\theta\, \approx\,\theta `` Hence,
    `` i=\mu\,A ``
  • Qstn #6
    Two cylinders `` A `` and `` B `` of equal capacity are connected to each other via a stop clock. A contains an ideal gas at standard temperature and pressure. `` B `` is completely evacuated. The entire system is thermally insulated. The stop clock is suddenly opened. The process is:
    (A)isothermal
    (B)adiabatic
    (C)isochoric
    (D)isobaric
    digAnsr:   B
    Ans : The entire system is completely insulated and the free expansion of the gas will take place, the temperature of the gas will remain constant. So the process will be adiabatic.
  • Qstn #7
    The energy equivalent of 0.5 g of a substance is:
    (A) `` 4.5 \times 10^{16} J ``
    (B) `` 4.5 \times 10^{13} J ``
    (C) `` 1.5 \times 10^{13} J ``
    (D) `` 0.5 \times 10^{13} J ``
    digAnsr:   B
    Ans : From mass-energy equivalence,
    `` E=mc^{2} ``
    `` =0.5\times 10^{-3}\times 9\times 10^{16} ``
    `` =4.5 \times 10^{13}\,J ``
  • Qstn #8
    A body weighs 72 N on the surface of the earth. What is the gravitational force on it, at a height equal to half the radius of the earth?
    (A)48 N
    (B)32 N
    (C)30 N
    (D)24 N
    digAnsr:   B
    Ans : `` w_{s}=mg_{s}=72\,N ``
    `` w_{h}=mg_{h}=\frac{mg_{s}}{\left(1+\frac{h}{R}\right)^{2}} ``
    `` =\frac{72\,N}{\left(1+\frac{R /2}{2}\right)} ``
    `` =\frac{72}{9 /4} ``
    `` w_{h}=32\,N ``
  • Qstn #9
    The solids which have negative temperature coefficient of resistance are :
    (A)metals
    (B)insulators only
    (C)semiconductors only
    (D)insulators and semiconductors
    digAnsr:   D
    Ans : For metals temperature coefficient of resistance is positive while for insulators and semiconductors, temperature coefficient of resistance is negative
  • Qstn #10
    The phase difference between displacement and acceleration of a particle in a simple harmonic motion is:
    (A) `` \pi `` rad
    (B) `` \frac {3\pi}{2} `` rad
    (C) `` \frac {\pi}{2} `` rad
    (D) `` zero ``
    digAnsr:   A
    Ans : Displacement (x) of SHM
    `` x=A\,sin \left(\omega t+\phi\right) \dots(i) ``
    `` \frac{dx}{dt}=A\,\omega\,cos(\omega\,t+\phi) ``
    Acceleration ``
    (a)=\frac{d^{2}x}{dt^{2}} ``
    `` \Rightarrow a=-\omega^{2}\,A\,sin(\omega\,t+\phi) ``
    `` \Rightarrow a=\omega^{2}\,A\,sin(\omega\,t+\phi+\pi)\dots(ii) ``
    from (1) & (2), phase difference between displacement and acceleration is `` \pi ``
  • Qstn #11
    A screw gauge has least count of 0.01 mm and there are 50 divisions in its circular scale.
    The pitch of the screw gauge is:
    (A)0.01 mm
    (B)0.25 mm
    (C)0.5 mm
    (D)1.0 mm
    digAnsr:   C
    Ans : L.C. `` =\frac{\text{Pitch}}{\text{Number of division on circular scale}} ``
    `` \Rightarrow 0.01\,mm=\frac{\text{pitch}}{50} ``
    `` \Rightarrow `` pitch `` =0.5\,mm ``
  • Qstn #12
    In a guitar, two strings A and B made of same material are slightly out of tune and produce beats of frequency `` 6\,Hz `` . When tension in B is slightly decreased, the be at frequency increases to `` 7\,Hz `` . If the frequency of A is `` 530\,Hz `` , the original frequency of B will be :
    (A)523 Hz
    (B)524 Hz
    (C)536 H z
    (D)537 H z
    digAnsr:   B
    Ans : It is given, the difference of `` f_{A} `` and `` f_{B} `` is `` 6\,HZ ``
    Guitar string i.e. string is fixed from both ends
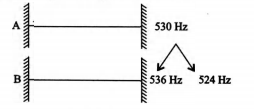
    image
    Frequency `` \propto \sqrt{\text{Tension}} ``
    If tension in B slightly decrease then frequency of B decreases
    If B is 536 Hz, as the frequency decreases, beats with A also decreases
    If B is 524 Hz, as the frequency decreases, beats with A increases
    If tension decreases, `` f_{B} `` decreases and becomes `` f'_{B} ``
    Now, difference of `` f_{A} `` and `` f'_{B}=7\,Hz `` (increases)
    So, `` f_{A}=f_{B} ``
    `` f_{A}-f_{B}=6\,Hz ``
    `` f_{A}=530\,Hz ``
    `` f_{B}=524\,Hz `` (original)
  • Qstn #13
    Two particles of mass `` 5\,kg `` and `` 10\,kg `` respectively are attached to the two ends of a rigid rod of length 1m with negligible mass.
    The centre of mass of the system from the `` 5\,kg `` particle is nearly at a distance of :
    (A)33 cm
    (B)50 cm
    (C)67 cm
    (D)80 cm
    digAnsr:   C
    Ans : Let position of centre of mass be `` {(x_{c.m}, 0)} ``
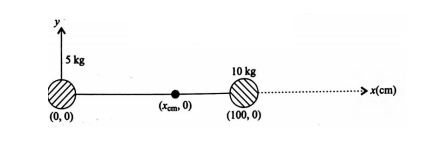
    image
    `` x_{cm}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}} ``
    `` =\frac{5 \times 0+100 \times 10}{5+10} ``
    `` =\frac{200}{2} ``
    `` =66.66\,cm ``
    `` x_{cm}=67\,cm ``
  • Qstn #14
    Find the torque about the origin when a force of `` 3 \,\hat{j}\, N `` acts on a particle whose position vector is `` 2\, \hat {k}\, m `` .
    (A) `` 6 \hat{i}\, Nm ``
    (B) `` 6 \hat{j} \,Nm ``
    (C) `` -6 \hat{i} \,Nm ``
    (D) `` 6 \hat{k} Nm ``
    digAnsr:   C
    Ans : Given: `` \vec{F}=3 \hat{j}\,N `` ,
    `` \vec{r}=2\hat{k} ``
    We know, `` \vec{\tau}=\vec{r}\times\vec{F}=2\hat{k}\times3\hat{j} ``
    `` =6\left(\hat{k} \times\hat{j}\right)=6\left(-\hat{i}\right) ``
    `` \vec{\tau}=-6 \hat{i}\,Nm ``
next page