NEET-XII-Physics
13: Nuclei
- #29Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 13.6. You are given that
m (198Au) = 197.968233 u
m (198Hg) =197.966760 u
Ans : It can be observed from the given γ-decay diagram that γ1 decays from the 1.088 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ1-decay is given as:
E1 = 1.088 - 0 = 1.088 MeV
hν1= 1.088 × 1.6 × 10-19 × 106 J
Where,
h = Planck’s constant = 6.6 × 10-34 Js
ν1 = Frequency of radiation radiated by γ1-decay
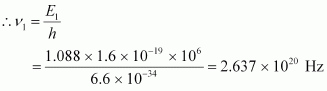
It can be observed from the given γ-decay diagram that γ2 decays from the 0.412 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ2-decay is given as:
E2 = 0.412 - 0 = 0.412 MeV
hν2= 0.412 × 1.6 × 10-19 × 106 J
Where,
ν2 = Frequency of radiation radiated by γ2-decay
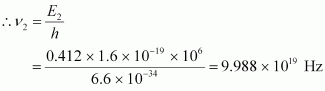
It can be observed from the given γ-decay diagram that γ3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to γ3-decay is given as:
E3 = 1.088 - 0.412 = 0.676 MeV
hν3= 0.676 × 10-19 × 106 J
Where,
ν3 = Frequency of radiation radiated by γ3-decay
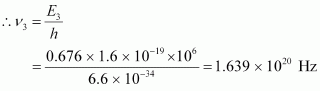
Mass of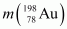
= 197.968233 u
Mass of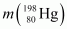
= 197.966760 u
1 u = 931.5 MeV/c2
Energy of the highest level is given as:
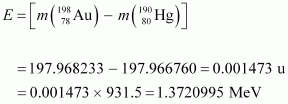
β1 decays from the 1.3720995 MeV level to the 1.088 MeV level
∴Maximum kinetic energy of the β1 particle = 1.3720995 - 1.088
= 0.2840995 MeV
β2 decays from the 1.3720995 MeV level to the 0.412 MeV level
∴Maximum kinetic energy of the β2 particle = 1.3720995 - 0.412
= 0.9600995 MeV