HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

11: Dual Nature Of Radiation And Matter

 page 4

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • #20
  • #20-a
    Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be 1.76 × 1011 C kg-1.
    Ans : Potential difference across the evacuated tube, V = 500 V

    Specific charge of an electron, e/m = 1.76 × 1011 C kg-1

    The speed of each emitted electron is given by the relation for kinetic energy as:



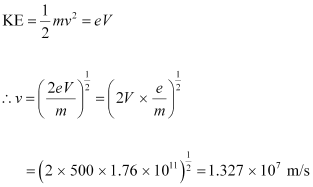
    Therefore, the speed of each emitted electron is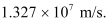
  • #20-b
    Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong? In what way is the formula to be modified?
    Ans : Potential of the anode, V = 10 MV = 10 × 106 V

    The speed of each electron is given as:



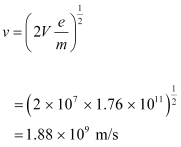
    This result is wrong because nothing can move faster than light. In the above formula, the expression (mv2/2) for energy can only be used in the non-relativistic limit, i.e., for v << c.

    For very high speed problems, relativistic equations must be considered for solving them. In the relativistic limit, the total energy is given as:

    E = mc2

    Where,

    m = Relativistic mass



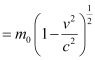
    m0 = Mass of the particle at rest

    Kinetic energy is given as:

    K = mc2 - m0c2
  • #21
  • #21-a
    A monoenergetic electron beam with electron speed of 5.20 × 106 m s-1 is subject to a magnetic field of 1.30 × 10-4 T normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals 1.76 × 1011 C kg-1.
    Ans : Speed of an electron, v = 5.20 × 106 m/s

    Magnetic field experienced by the electron, B = 1.30 × 10-4 T

    Specific charge of an electron, e/m = 1.76 × 1011 C kg-1

    Where,

    e = Charge on the electron = 1.6 × 10-19 C

    m = Mass of the electron = 9.1 × 10-31 kg-1

    The force exerted on the electron is given as:



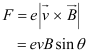
    θ = Angle between the magnetic field and the beam velocity

    The magnetic field is normal to the direction of beam.



    The beam traces a circular path of radius, r. It is the magnetic field, due to its bending nature, that provides the centripetal force for the beam.

    Hence, equation (1) reduces to:



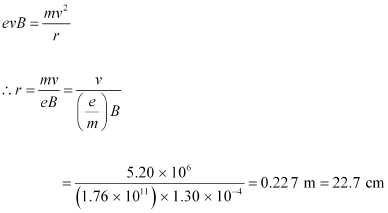
    Therefore, the radius of the circular path is 22.7 cm.
  • #21-b
    Is the formula you employ in (a) valid for calculating radius of the path of a 20 MeV electron beam? If not, in what way is it modified?

    [Note: Exercises 11.20(b) and 11.21(b) take you to relativistic mechanics which is beyond the scope of this book. They have been inserted here simply to emphasise the point that the formulas you use in part (a) of the exercises are not valid at very high speeds or energies. See answers at the end to know what ‘very high speed or energy’ means.]
    Ans : Energy of the electron beam, E = 20 MeV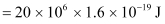

    The energy of the electron is given as:



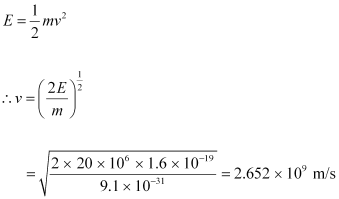
    This result is incorrect because nothing can move faster than light. In the above formula, the expression (mv2/2) for energy can only be used in the non-relativistic limit, i.e., for v << c

    When very high speeds are concerned, the relativistic domain comes into consideration.

    In the relativistic domain, mass is given as:



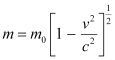
    Where,

    = Mass of the particle at rest

    Hence, the radius of the circular path is given as:


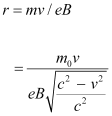
  • Qstn #22
    An electron gun with its collector at a potential of 100 V fires out electrons in a spherical bulb containing hydrogen gas at low pressure (∼10-2 mm of Hg). A magnetic field of 2.83 × 10-4 T curves the path of the electrons in a circular orbit of radius 12.0 cm. (The path can be viewed because the gas ions in the path focus the beam by attracting electrons, and emitting light by electron capture; this method is known as the ‘fine beam tube’ method. Determine e/m from the data.
    Ans : Potential of an anode, V = 100 V

    Magnetic field experienced by the electrons, B = 2.83 × 10-4 T

    Radius of the circular orbit r = 12.0 cm = 12.0 × 10-2 m

    Mass of each electron = m

    Charge on each electron = e

    Velocity of each electron = v

    The energy of each electron is equal to its kinetic energy, i.e.,



    It is the magnetic field, due to its bending nature, that provides the centripetal force for the beam. Hence, we can write:

    Centripetal force = Magnetic force



    Putting the value of v in equation (1), we get:



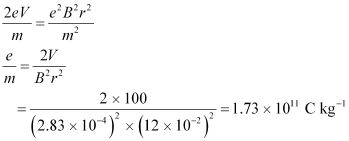
    Therefore, the specific charge ratio (e/m) is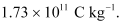
  • #23
  • #23-a
    An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.45 Ã…. What is the maximum energy of a photon in the radiation?
    Ans : Wavelength produced by an X-ray tube,

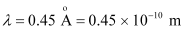
    Planck’s constant, h = 6.626 × 10-34 Js

    Speed of light, c = 3 × 108 m/s

    The maximum energy of a photon is given as:



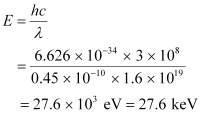
    Therefore, the maximum energy of an X-ray photon is 27.6 keV.
  • #23-b
    From your answer to (a), guess what order of accelerating voltage (for electrons) is required in such a tube?
    Ans : Accelerating voltage provides energy to the electrons for producing X-rays. To get an X-ray of 27.6 keV, the incident electrons must possess at least 27.6 keV of kinetic electric energy. Hence, an accelerating voltage of the order of 30 keV is required for producing X-rays.
  • Qstn #24
    In an accelerator experiment on high-energy collisions of electrons with positrons, a certain event is interpreted as annihilation of an electron-positron pair of total energy 10.2 BeV into two γ-rays of equal energy. What is the wavelength associated with each γ-ray? (1BeV = 109 eV)
    Ans : Total energy of two γ-rays:

    E = 10. 2 BeV

    = 10.2 × 109 eV

    = 10.2 × 109 × 1.6 × 10-10 J

    Hence, the energy of each γ-ray:



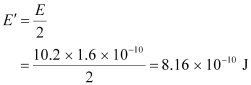
    Planck’s constant,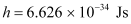

    Speed of light,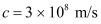

    Energy is related to wavelength as:



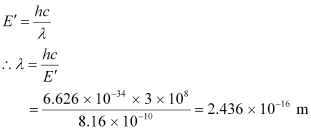
    Therefore, the wavelength associated with each γ-ray is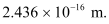
  • Qstn #25
    Estimating the following two numbers should be interesting. The first number will tell you why radio engineers do not need to worry much about photons! The second number tells you why our eye can never ‘count photons’, even in barely detectable light.
  • #25-a
    The number of photons emitted per second by a Medium wave transmitter of 10 kW power, emitting radiowaves of wavelength 500 m.
    Ans : Power of the medium wave transmitter, P = 10 kW = 104 W = 104 J/s

    Hence, energy emitted by the transmitter per second, E = 104

    Wavelength of the radio wave, λ = 500 m

    The energy of the wave is given as:



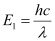
    Where,

    h = Planck’s constant = 6.6 × 10-34 Js

    c = Speed of light = 3 × 108 m/s



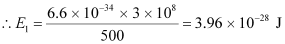
    Let n be the number of photons emitted by the transmitter.

    ∴nE1 = E



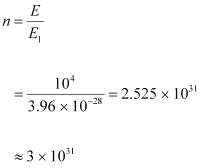
    The energy (E1) of a radio photon is very less, but the number of photons (n) emitted per second in a radio wave is very large.

    The existence of a minimum quantum of energy can be ignored and the total energy of a radio wave can be treated as being continuous.
  • #25-b
    The number of photons entering the pupil of our eye per second corresponding to the minimum intensity of white light that we humans can perceive (∼10-10 W m-2). Take the area of the pupil to be about 0.4 cm2, and the average frequency of white light to be about 6 × 1014 Hz.
    Ans : Intensity of light perceived by the human eye, I = 10-10 W m-2

    Area of a pupil, A = 0.4 cm2 = 0.4 × 10-4 m2

    Frequency of white light, ν= 6 × 1014 Hz

    The energy emitted by a photon is given as:

    E = hν

    Where,

    h = Planck’s constant = 6.6 × 10-34 Js

    ∴E = 6.6 × 10-34 × 6 × 1014

    = 3.96 × 10-19 J

    Let n be the total number of photons falling per second, per unit area of the pupil.

    The total energy per unit for n falling photons is given as:

    E = n × 3.96 × 10-19 J s-1 m-2

    The energy per unit area per second is the intensity of light.

    ∴E = I

    n × 3.96 × 10-19 = 10-10



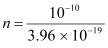
    = 2.52 × 108 m2 s-1

    The total number of photons entering the pupil per second is given as:

    nA = n × A

    = 2.52 × 108 × 0.4 × 10-4

    = 1.008 × 104 s-1

    This number is not as large as the one found in problem (a), but it is large enough for the human eye to never see the individual photons.
  • Qstn #26
    Ultraviolet light of wavelength 2271 Å from a 100 W mercury source irradiates a photo-cell made of molybdenum metal. If the stopping potential is -1.3 V, estimate the work function of the metal. How would the photo-cell respond to a high intensity (∼105 W m-2) red light of wavelength 6328 Å produced by a He-Ne laser?
    Ans : Wavelength of ultraviolet light, λ = 2271 Å = 2271 × 10-10 m

    Stopping potential of the metal, V0 = 1.3 V

    Planck’s constant, h = 6.6 × 10-34 J

    Charge on an electron, e = 1.6 × 10-19 C

    Work function of the metal =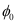

    Frequency of light = ν

    We have the photo-energy relation from the photoelectric effect as:

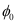    = hν - eV0



    Let ν0 be the threshold frequency of the metal.

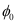    ∴= hν0



    Wavelength of red light, = 6328 × 10-10 m

    ∴Frequency of red light,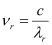



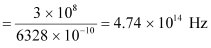
    Since ν0> νr, the photocell will not respond to the red light produced by the laser.
next page