HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

11: Dual Nature Of Radiation And Matter

 page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #7
    A 100 W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is 589 nm.
    Ans : Power of the sodium lamp, P = 100 W

    Wavelength of the emitted sodium light, λ = 589 nm = 589 × 10-9 m

    Planck’s constant, h = 6.626 × 10-34 Js

    Speed of light, c = 3 × 108 m/s
  • #7-a
    What is the energy per photon associated with the sodium light?
    Ans : The energy per photon associated with the sodium light is given as:




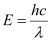
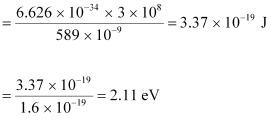
  • #7-b
    At what rate are the photons delivered to the sphere?
    Ans : Number of photons delivered to the sphere = n

    The equation for power can be written as:



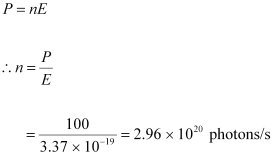
    Therefore, every second,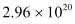 photons are delivered to the sphere.
  • Qstn #8
    The threshold frequency for a certain metal is 3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal, predict the cutoff voltage for the photoelectric emission.
    Ans : Threshold frequency of the metal,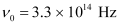

    Frequency of light incident on the metal,

    Charge on an electron, e = 1.6 × 10-19 C

    Planck’s constant, h = 6.626 × 10-34 Js

    Cut-off voltage for the photoelectric emission from the metal =

    The equation for the cut-off energy is given as:



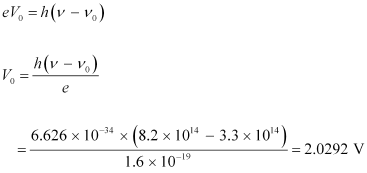
    Therefore, the cut-off voltage for the photoelectric emission is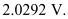
  • Qstn #9
    The work function for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm?
    Ans : No

    Work function of the metal,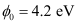

    Charge on an electron, e = 1.6 × 10-19 C

    Planck’s constant, h = 6.626 × 10-34 Js

    Wavelength of the incident radiation, λ = 330 nm = 330 × 10-9 m

    Speed of light, c = 3 × 108 m/s

    The energy of the incident photon is given as:



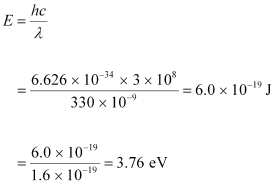
    It can be observed that the energy of the incident radiation is less than the work function of the metal. Hence, no photoelectric emission will take place.
  • Qstn #10
    Light of frequency 7.21 × 1014 Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 105 m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
    Ans : Frequency of the incident photon,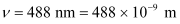

    Maximum speed of the electrons, v = 6.0 × 105 m/s

    Planck’s constant, h = 6.626 × 10-34 Js

    Mass of an electron, m = 9.1 × 10-31 kg

    For threshold frequency ν0, the relation for kinetic energy is written as:



    Therefore, the threshold frequency for the photoemission of electrons is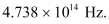
  • Qstn #11
    Light of wavelength 488 nm is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut-off) potential of photoelectrons is 0.38 V. Find the work function of the material from which the emitter is made.
    Ans : Wavelength of light produced by the argon laser, λ = 488 nm

    = 488 × 10-9 m

    Stopping potential of the photoelectrons, V0 = 0.38 V

    1eV = 1.6 × 10-19 J

    ∴ V0 =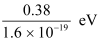

    Planck’s constant, h = 6.6 × 10-34 Js

    Charge on an electron, e = 1.6 × 10-19 C

    Speed of light, c = 3 × 10 m/s

    From Einstein’s photoelectric effect, we have the relation involving the work function Φ0 of the material of the emitter as:



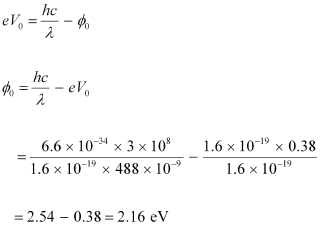
    Therefore, the material with which the emitter is made has the work function of 2.16 eV.
  • Qstn #12
    Calculate the
    Ans : Potential difference, V = 56 V

    Planck’s constant, h = 6.6 × 10-34 Js

    Mass of an electron, m = 9.1 × 10-31 kg

    Charge on an electron, e = 1.6 × 10-19 C
  • #12-a
    momentum, and
    Ans : At equilibrium, the kinetic energy of each electron is equal to the accelerating potential, i.e., we can write the relation for velocity (v) of each electron as:



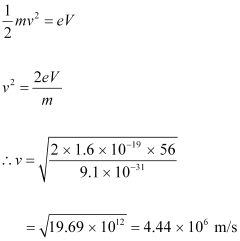
    The momentum of each accelerated electron is given as:

    p = mv

    = 9.1 × 10-31 × 4.44 × 106

    = 4.04 × 10-24 kg m s-1

    Therefore, the momentum of each electron is 4.04 × 10-24 kg m s-1.
  • #12-b
    de Broglie wavelength of the electrons accelerated through a potential difference of 56 V.
    Ans : De Broglie wavelength of an electron accelerating through a potential V, is given by the relation:





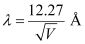
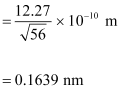
    Therefore, the de Broglie wavelength of each electron is 0.1639 nm.
  • Qstn #13
    What is the
    Ans : Kinetic energy of the electron, Ek = 120 eV

    Planck’s constant, h = 6.6 × 10-34 Js

    Mass of an electron, m = 9.1 × 10-31 kg

    Charge on an electron, e = 1.6 × 10-19 C
  • #13-a
    momentum,
    Ans : For the electron, we can write the relation for kinetic energy as:



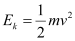
    Where,

    v = Speed of the electron



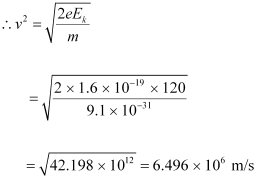
    Momentum of the electron, p = mv

    = 9.1 × 10-31 × 6.496 × 106

    = 5.91 × 10-24 kg m s-1

    Therefore, the momentum of the electron is 5.91 × 10-24 kg m s-1.
  • #13-b
    speed, and
    Ans : Speed of the electron, v = 6.496 × 106 m/s
  • #13-c
    de Broglie wavelength of an electron with kinetic energy of 120 eV.
    Ans : De Broglie wavelength of an electron having a momentum p, is given as:



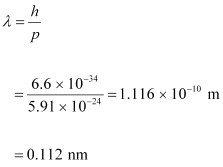
    Therefore, the de Broglie wavelength of the electron is 0.112 nm.
  • Qstn #14
    The wavelength of light from the spectral emission line of sodium is 589 nm. Find the kinetic energy at which
    Ans : Wavelength of light of a sodium line, λ = 589 nm = 589 × 10-9 m

    Mass of an electron, me= 9.1 × 10-31 kg

    Mass of a neutron, mn= 1.66 × 10-27 kg

    Planck’s constant, h = 6.6 × 10-34 Js
next page