NEET-XII-Physics
09: Ray Optics And Optical Instruments
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #32-dWhy must both the objective and the eyepiece of a compound microscope have short focal lengths?Ans : The angular magnification produced by the eyepiece of a compound microscope is
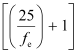
Where,
fe = Focal length of the eyepiece
It can be inferred that if fe is small, then angular magnification of the eyepiece will be large.
The angular magnification of the objective lens of a compound microscope is given as
Where,
 = Object distance for the objective lens
= Object distance for the objective lens
 = Focal length of the objective
= Focal length of the objective
The magnification is large when >
> . In the case of a microscope, the object is kept close to the objective lens. Hence, the object distance is very little. Since
. In the case of a microscope, the object is kept close to the objective lens. Hence, the object distance is very little. Since  is small,
is small,  will be even smaller. Therefore,
will be even smaller. Therefore,  and
and  are both small in the given condition.
are both small in the given condition.
- #32-eWhen viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?Ans : When we place our eyes too close to the eyepiece of a compound microscope, we are unable to collect much refracted light. As a result, the field of view decreases substantially. Hence, the clarity of the image gets blurred.
The best position of the eye for viewing through a compound microscope is at the eye-ring attached to the eyepiece. The precise location of the eye depends on the separation between the objective lens and the eyepiece.
- Qstn #33An angular magnification (magnifying power) of 30X is desired using an objective of focal length 1.25 cm and an eyepiece of focal length 5 cm. How will you set up the compound microscope?
Ans : Focal length of the objective lens,.gif) = 1.25 cm
= 1.25 cm
Focal length of the eyepiece, fe = 5 cm
Least distance of distinct vision, d = 25 cm
Angular magnification of the compound microscope = 30X
Total magnifying power of the compound microscope, m = 30
The angular magnification of the eyepiece is given by the relation:
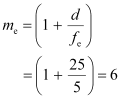
The angular magnification of the objective lens (mo) is related to me as:
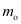
 = m
= m

Applying the lens formula for the objective lens:
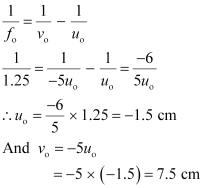
The object should be placed 1.5 cm away from the objective lens to obtain the desired magnification.
Applying the lens formula for the eyepiece:
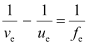
Where,
 = Image distance for the eyepiece = -d = -25 cm
= Image distance for the eyepiece = -d = -25 cm
.gif) = Object distance for the eyepiece
= Object distance for the eyepiece
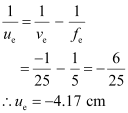
Separation between the objective lens and the eyepiece

Therefore, the separation between the objective lens and the eyepiece should be 11.67 cm.
- Qstn #34A small telescope has an objective lens of focal length 140 cm and an eyepiece of focal length 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when
Ans : Focal length of the objective lens,.gif) = 140 cm
= 140 cm
Focal length of the eyepiece, fe = 5 cm
Least distance of distinct vision, d = 25 cm
- #34-athe telescope is in normal adjustment (i.e., when the final image
is at infinity)?
Ans : When the telescope is in normal adjustment, its magnifying power is given as:
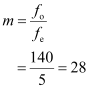
- #34-bthe final image is formed at the least distance of distinct vision
(25 cm)?
Ans : When the final image is formed at d,the magnifying power of the telescope is given as:

- #35Ans : Focal length of the objective lens, fo = 140 cm
Focal length of the eyepiece, fe = 5 cm
- #35-aFor the telescope described in Exercise 9.34 (a), what is the separation between the objective lens and the eyepiece?Ans : In normal adjustment, the separation between the objective lens and the eyepiece
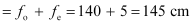
- #35-bIf this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens?Ans : Height of the tower, h1 = 100 m
Distance of the tower (object) from the telescope, u = 3 km = 3000 m
The angle subtended by the tower at the telescope is given as:
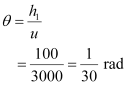
The angle subtended by the image produced by the objective lens is given as:
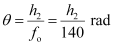
Where,
h2 = Height of the image of the tower formed by the objective lens
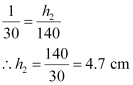
Therefore, the objective lens forms a 4.7 cm tall image of the tower.
- #35-cWhat is the height of the final image of the tower if it is formed at 25 cm?Ans : Image is formed at a distance, d = 25 cm
The magnification of the eyepiece is given by the relation:
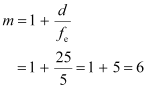
Height of the final image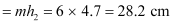
Hence, the height of the final image of the tower is 28.2 cm.
- Qstn #36A Cassegrain telescope uses two mirrors as shown in Fig. 9.33. Such a telescope is built with the mirrors 20 mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?
Ans : The following figure shows a Cassegrain telescope consisting of a concave mirror and a convex mirror.

Distance between the objective mirror and the secondary mirror, d = 20 mm
Radius of curvature of the objective mirror, R1 = 220 mm
Hence, focal length of the objective mirror,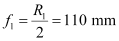
Radius of curvature of the secondary mirror, R1 = 140 mm
Hence, focal length of the secondary mirror,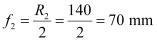
The image of an object placed at infinity, formed by the objective mirror, will act as a virtual object for the secondary mirror.
Hence, the virtual object distance for the secondary mirror,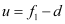
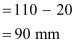
Applying the mirror formula for the secondary mirror, we can calculate image distance (v)as:
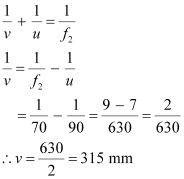
Hence, the final image will be formed 315 mm away from the secondary mirror.
- Qstn #37Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. 9.36. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?
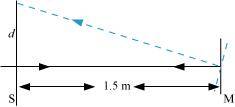
Ans : Angle of deflection, θ = 3.5°
Distance of the screen from the mirror, D = 1.5 m
The reflected rays get deflected by an amount twice the angle of deflection i.e., 2θ= 7.0°
The displacement (d) of the reflected spot of light on the screen is given as:
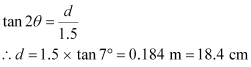
Hence, the displacement of the reflected spot of light is 18.4 cm.
- Qstn #38Figure 9.37 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid?
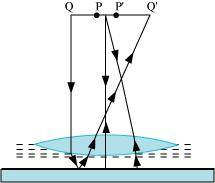
Ans : Focal length of the convex lens, f1 = 30 cm
The liquid acts as a mirror. Focal length of the liquid = f2
Focal length of the system (convex lens + liquid), f = 45 cm
For a pair of optical systems placed in contact, the equivalent focal length is given as:
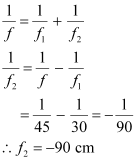
Let the refractive index of the lens be and the radius of curvature of one surface be R. Hence, the radius of curvature of the other surface is -R.
and the radius of curvature of one surface be R. Hence, the radius of curvature of the other surface is -R.
R can be obtained using the relation:
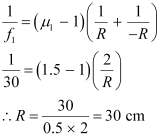
Let.gif) be the refractive index of the liquid.
be the refractive index of the liquid.
Radius of curvature of the liquid on the side of the plane mirror =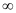
Radius of curvature of the liquid on the side of the lens, R = -30 cm
The value of.gif) can be calculated using the relation:
can be calculated using the relation:
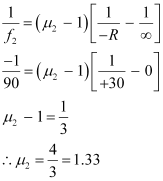
Hence, the refractive index of the liquid is 1.33.