HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

09: Ray Optics And Optical Instruments

II - page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #13
    A small telescope has an objective lens of focal length 144 cm and an eyepiece of focal length 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?
    Ans : Focal length of the objective lens, fo = 144 cm

    Focal length of the eyepiece, fe = 6.0 cm

    The magnifying power of the telescope is given as:



    The separation between the objective lens and the eyepiece is calculated as:





    Hence, the magnifying power of the telescope is 24 and the separation between the objective lens and the eyepiece is 150 cm.
  • #14
    Ans : Focal length of the objective lens, fo = 15 m = 15 × 102 cm

    Focal length of the eyepiece, fe = 1.0 cm
  • #14-a
    A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
    Ans : The angular magnification of a telescope is given as:



    Hence, the angular magnification of the given refracting telescope is 1500.
  • #14-b
    If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.48 × 106 m, and the radius of lunar orbit is 3.8 × 108 m.
    Ans : Diameter of the moon, d = 3.48 × 106 m

    Radius of the lunar orbit, r0 = 3.8 × 108 m

    Let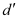 be the diameter of the image of the moon formed by the objective lens.

    The angle subtended by the diameter of the moon is equal to the angle subtended by the image.



    Hence, the diameter of the moon’s image formed by the objective lens is 13.74 cm
  • Qstn #15
    Use the mirror equation to deduce that:
  • #15-a
    an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
    Ans : For a concave mirror, the focal length (f) is negative.

    ∴f < 0

    When the object is placed on the left side of the mirror, the object distance (u) is negative.

    ∴u < 0

    For image distance v, we can write the lens formula as:



    The object lies between f and 2f.



    Using equation (1), we get:



    ∴ is negative, i.e., v is negative.



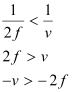
    Therefore, the image lies beyond 2f.
  • #15-b
    a convex mirror always produces a virtual image independent of the location of the object.
    Ans : For a convex mirror, the focal length (f) is positive.

    ∴ f > 0

    When the object is placed on the left side of the mirror, the object distance (u) is negative.

    ∴ u < 0

    For image distance v, we have the mirror formula:



    Thus, the image is formed on the back side of the mirror.

    Hence, a convex mirror always produces a virtual image, regardless of the object distance.
  • #15-c
    the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
    Ans : For a convex mirror, the focal length (f) is positive.

    ∴f > 0

    When the object is placed on the left side of the mirror, the object distance (u) is negative,

    ∴u < 0

    For image distance v, we have the mirror formula:



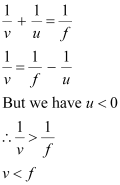
    Hence, the image formed is diminished and is located between the focus (f) and the pole.
  • #15-d
    an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.

    [Note: This exercise helps you deduce algebraically properties of

    images that one obtains from explicit ray diagrams.]
    Ans : For a concave mirror, the focal length (f) is negative.

    ∴f < 0

    When the object is placed on the left side of the mirror, the object distance (u) is negative.

    ∴u < 0

    It is placed between the focus (f) and the pole.



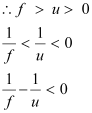
    For image distance v, we have the mirror formula:



    The image is formed on the right side of the mirror. Hence, it is a virtual image.

    For u < 0 and v > 0, we can write:



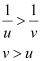
    Magnification, m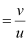 > 1

    Hence, the formed image is enlarged.
  • Qstn #16
    A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
    Ans : Actual depth of the pin, d = 15 cm

    Apparent dept of the pin =

    Refractive index of glass,

    Ratio of actual depth to the apparent depth is equal to the refractive index of glass, i.e.



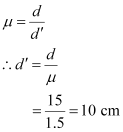
    The distance at which the pin appears to be raised =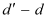



    For a small angle of incidence, this distance does not depend upon the location of the slab.
  • #17
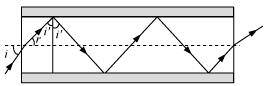
  • #17-a
    Figure 9.35 shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
    Ans : Refractive index of the glass fibre,

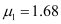
    Refractive index of the outer covering of the pipe,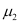 = 1.44

    Angle of incidence = i

    Angle of refraction = r

    Angle of incidence at the interface = i’

    The refractive index (μ) of the inner core - outer core interface is given as:



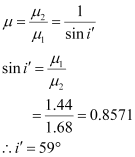
    For the critical angle, total internal reflection (TIR) takes place only when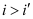, i.e., i > 59°

    Maximum angle of reflection,

    Let,

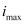    be the maximum angle of incidence.

    The refractive index at the air - glass interface,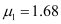

    We have the relation for the maximum angles of incidence and reflection as:



    Thus, all the rays incident at angles lying in the range 0 < i < 60° will suffer total internal reflection.
  • #17-b
    What is the answer if there is no outer covering of the pipe?


    Ans : If the outer covering of the pipe is not present, then:

    Refractive index of the outer pipe,

    For the angle of incidence i = 90°, we can write Snell’s law at the air - pipe interface as:

    .
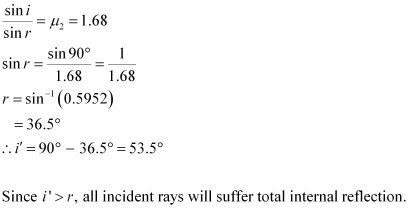  • #18-a
    You have learnt that plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain.
    Ans : Yes

    Plane and convex mirrors can produce real images as well. If the object is virtual, i.e., if the light rays converging at a point behind a plane mirror (or a convex mirror) are reflected to a point on a screen placed in front of the mirror, then a real image will be formed.
next page