NEET-XII-Physics
04: Moving Charges And Magnetism
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #13
- #13-aA circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.Ans : Number of turns on the circular coil, n = 30
Radius of the coil, r = 8.0 cm = 0.08 m
Area of the coil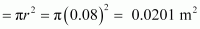
Current flowing in the coil, I = 6.0 A
Magnetic field strength, B = 1 T
Angle between the field lines and normal with the coil surface,
θ = 60°
The coil experiences a torque in the magnetic field. Hence, it turns. The counter torque applied to prevent the coil from turning is given by the relation,
τ = n IBA sinθ ... (i)
= 30 × 6 × 1 × 0.0201 × sin60°
= 3.133 N m
- #13-bWould your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)Ans : It can be inferred from relation (i) that the magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. Hence, the answer would not change if the circular coil in the above case is replaced by a planar coil of some irregular shape that encloses the same area.
- Qstn #14Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
Ans : Radius of coil X, r1 = 16 cm = 0.16 m
Radius of coil Y, r2 = 10 cm = 0.1 m
Number of turns of on coil X, n1 = 20
Number of turns of on coil Y, n2 = 25
Current in coil X, I1 = 16 A
Current in coil Y, I2 = 18 A
Magnetic field due to coil X at their centre is given by the relation,
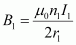
Where,
.gif) = Permeability of free space =
= Permeability of free space = 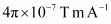
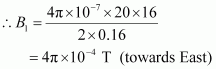
Magnetic field due to coil Y at their centre is given by the relation,
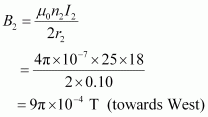
Hence, net magnetic field can be obtained as:
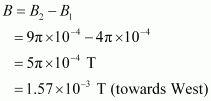
- Qstn #15A magnetic field of 100 G (1 G = 10-4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10-3 m2. The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m-1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic
Ans : Magnetic field strength, B = 100 G = 100 × 10-4 T
Number of turns per unit length, n = 1000 turns m-1
Current flowing in the coil, I = 15 A
Permeability of free space,.gif) =
= .gif)
Magnetic field is given by the relation,
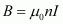
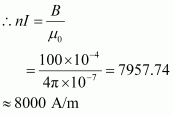
If the length of the coil is taken as 50 cm, radius 4 cm, number of turns 400, and current 10 A, then these values are not unique for the given purpose. There is always a possibility of some adjustments with limits.
- Qstn #16For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
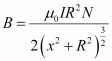
Ans : Radius of circular coil = R
Number of turns on the coil = N
Current in the coil = I
Magnetic field at a point on its axis at distance x is given by the relation,
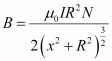
Where,
.gif) = Permeability of free space
= Permeability of free space
- #16-aShow that this reduces to the familiar result for field at the centre of the coil.Ans : If the magnetic field at the centre of the coil is considered, then x = 0.
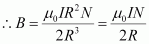
This is the familiar result for magnetic field at the centre of the coil.
- #16-bConsider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
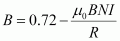 , approximately.
, approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Ans : Radii of two parallel co-axial circular coils = R
Number of turns on each coil = N
Current in both coils = I
Distance between both the coils = R
Let us consider point Q at distance d from the centre.
Then, one coil is at a distance of from point Q.
from point Q.
.gif) Magnetic field at point Q is given as:
Magnetic field at point Q is given as:
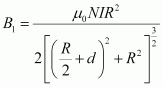
Also, the other coil is at a distance of from point Q.
from point Q.
.gif) Magnetic field due to this coil is given as:
Magnetic field due to this coil is given as:
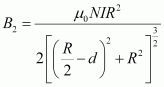
Total magnetic field,
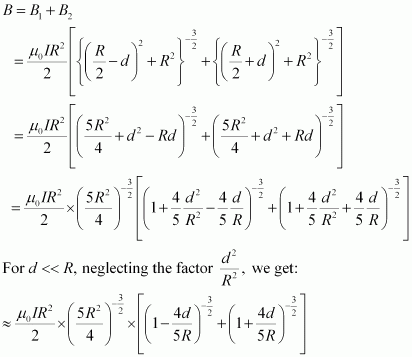

Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.
- Qstn #17A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic fieldAns : Inner radius of the toroid, r1 = 25 cm = 0.25 m
Outer radius of the toroid, r2 = 26 cm = 0.26 m
Number of turns on the coil, N = 3500
Current in the coil, I = 11 A
- #17-aoutside the toroid,Ans : Magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.
- #17-binside the core of the toroid, andAns : Magnetic field inside the core of a toroid is given by the relation,
B =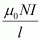
Where,
.gif) = Permeability of free space =
= Permeability of free space = .gif)
l = length of toroid

- #17-cin the empty space surrounded by the toroid.Ans : Magnetic field in the empty space surrounded by the toroid is zero.
- #18-aA magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?Ans : The initial velocity of the particle is either parallel or anti-parallel to the magnetic field. Hence, it travels along a straight path without suffering any deflection in the field.
- #18-bA charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?Ans : Yes, the final speed of the charged particle will be equal to its initial speed. This is because magnetic force can change the direction of velocity, but not its magnitude.