NEET-XII-Physics
04: Moving Charges And Magnetism
- #16For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
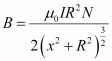
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
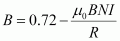, approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Ans : Radius of circular coil = R
Number of turns on the coil = N
Current in the coil = I
Magnetic field at a point on its axis at distance x is given by the relation,
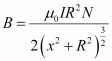
Where,
.gif)
= Permeability of free space
(a) If the magnetic field at the centre of the coil is considered, then x = 0.
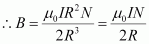
This is the familiar result for magnetic field at the centre of the coil.
(b) Radii of two parallel co-axial circular coils = R
Number of turns on each coil = N
Current in both coils = I
Distance between both the coils = R
Let us consider point Q at distance d from the centre.
Then, one coil is at a distance of
from point Q.
.gif)
Magnetic field at point Q is given as:
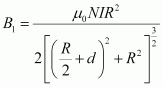
Also, the other coil is at a distance of
from point Q.
Magnetic field due to this coil is given as:
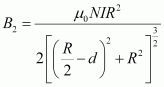
Total magnetic field,
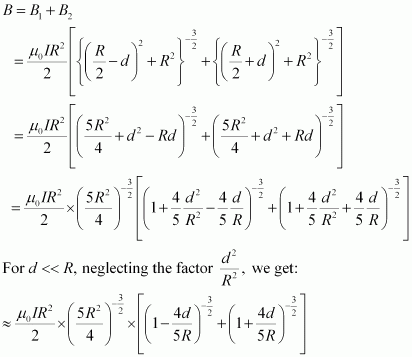
Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.
- #16-aShow that this reduces to the familiar result for field at the centre of the coil.Ans : If the magnetic field at the centre of the coil is considered, then x = 0.
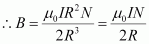
This is the familiar result for magnetic field at the centre of the coil.
- #16-bConsider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
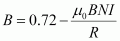, approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Ans : Radii of two parallel co-axial circular coils = R
Number of turns on each coil = N
Current in both coils = I
Distance between both the coils = R
Let us consider point Q at distance d from the centre.
Then, one coil is at a distance offrom point Q.
Magnetic field at point Q is given as:
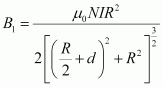
Also, the other coil is at a distance offrom point Q.
Magnetic field due to this coil is given as:
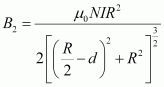
Total magnetic field,
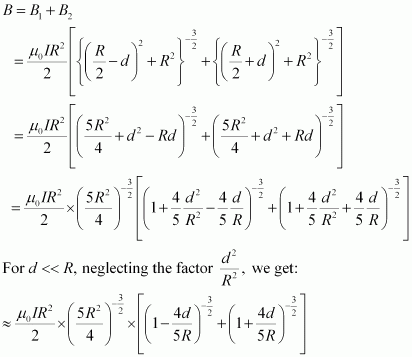
Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.