HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
CBSE-XI-Physics

05: Newton's Laws of Motion

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #6
    The force exerted by the floor of an elevator on the foot of a person is more than the weight of the person if the elevator is
    (a) going up and slowing down
    (b) going up and speeding up
    (c) going down and slowing down
    (d) going down and speeding up
    digAnsr:   b,c
    Ans : (b) going up and speeding up
    (c) going down and slowing down
    It means normal force exerted by the floor of the elevator on the person is greater that the weight of the person.
    i.e. N > mg
    (i) Going up and speeding up:
    aeff = g + a
    N = maeff = mg + ma (N > mg)
    (ii) Going down and speeding up:
    aeff = g - a
    N = mg - ma (N < mg)
    (iii) Going down and slowing down:
    aeff = g - (-a) = g + a
    N = mg + ma (N > mg)
    (iv) Going up and slowing down:
    aeff = g - a
    N = mg - ma (N < mg)
    Page No 79:
  • Qstn #7
    If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
    (a) going up with increasing speed
    (b) going down with increasing speed
    (c) going up with uniform speed
    (d) going down with uniform speed
    digAnsr:   c,d
    Ans : (c) going up with uniform speed
    (d) going down with uniform speed
    Tension in the cable = Weight of the elevator
    Or, total upward force = total downward force
    That is, there's no acceleration or uniform velocity.
    So, the elevator is going up/down with uniform speed.
    Page No 79:
  • Qstn #8
    A particle is observed from two frames S1 and S2. Frame S2 moves with respect to S1 with an acceleration a. Let F1 and F2 be the pseudo forces on the particle when seen from S1 and S2, respectively. Which of the following is not possible?
    (a) F1 = 0, F2 ≠ 0
    (b) F1 ≠ 0, F2 = 0
    (c) F1 ≠ 0, F2 ≠ 0
    (d) F1 = 0, F2 = 0
    digAnsr:   d
    Ans : (d) F1 = 0, F2 = 0
    `` {a}_{{s}_{2}{s}_{1}}=a...\left(1\right)``
    Acceleration of the particle w.r.t. to S1 = F1/m
    Acceleration of the particle w.r.t. to S2 = F2/m
    If we assume F1 = 0 and F2 = 0,
    we can conclude that `` {a}_{{s}_{2}{s}_{1}}=0...\left(2\right)``
    From equations (1) and (2), we can say that our assumption is wrong.
    And F1 = 0, F2 = 0 is not possible.
    Page No 79:
  • Qstn #9
    A person says that he measured the acceleration of a particle to be non-zero even though no force was acting on the particle.
    (a) He is a liar.
    (b) His clock might have run slow.
    (c) His metre scale might have been longer than the standard.
    (d) He might have used a non-inertial frame.
    digAnsr:   d
    Ans : (d) He might have used a non-inertial frame
    If no force is acting on a particle and yet, its acceleration is non-zero, it means the observer is in a non-inertial frame.
    Page No 79:
  • #
    Section : iv
  • Qstn #1
    A block of mass 2 kg placed on a long frictionless horizontal table is pulled horizontally by a constant force F. It is found to move 10 m in the first seconds. Find the magnitude of F.
    Ans : Given:
    Mass of the block, m = 2 kg,
    Distance covered, S = 10 m and initial velocity, u = 0
    Let a be the acceleration of the block.
    Using, `` \,\mathrm{\,S \,}=ut+\frac{1}{2}a{t}^{2}``, we get:
    `` 10=\frac{1}{2}a\left({2}^{2}\right)``
    `` \Rightarrow 10=2a``
    `` \Rightarrow a=5\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    ∴ Force, F = ma = 2 × 5 = 10 N
    Page No 79:
  • Qstn #2
    A car moving at 40 km/hr is to be stopped by applying brakes in the next 4 m. If the car weighs 2000 kg, what average force must be applied to stop it?
    Ans : Given:
    Initial speed of the car, u = 40 km/hr `` =\frac{4000}{3600}=11.11\,\mathrm{\,m \,}/\,\mathrm{\,s \,}``
    Final speed of the car, v = 0
    Mass of the car, m = 2000 kg
    Distance to be travelled by the car before coming to rest, s = 4m
    Acceleration, `` a=\frac{{v}^{2}-{u}^{2}}{2\,\mathrm{\,s \,}}``
    `` \Rightarrow a=\frac{{0}^{2}-{\left(11.11\right)}^{2}}{2\times 4}=\frac{-123.43}{8}=-15.42\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    ∴ Average force to be applied to stop the car, F = ma
    ⇒ F = 2000 × 15.42 ≈ 3.1 × 104 N
    Page No 79:
  • Qstn #3
    In a TV picture tube, electrons are ejected from the cathode with negligible speed and they attain a velocity of 5 × 106 m/s in travelling one centimetre. Assuming straight-line motion, find the constant force exerted on the electrons. The mass of an electron is 9.1 × 10-31 kg.
    Ans : Initial velocity of the electrons is negligible, i.e. u = 0.
    Final velocity of the electrons, v = 5 × 106 m/s
    Distance travelled by the electrons,
    s = 1 cm = 1 × 10-2 m
    ∴ Acceleration, `` a=\frac{{v}^{2}-{u}^{2}}{2\,\mathrm{\,S \,}}``
    `` \Rightarrow a=\frac{{\left(5\times {10}^{5}\right)}^{2}-0}{2\times 1\times {10}^{-3}}=\frac{25\times {10}^{12}}{2\times {10}^{-2}}``
    `` \Rightarrow a=12.5\times {10}^{14}\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    So, force on the electrons, F = ma
    ⇒ F = 9.1 × 10-31 × 12.5 × 10-14
    = 1.1 × 10-15 N
    Page No 79:
  • Qstn #4
    A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
    Ans : The free-body diagrams for both the blocks are shown below:

    From the free-body diagram of the 0.3 kg block,
    T = 0.3g
    ⇒ T= 0.3 × 10 = 3 N
    Now, from the free-body diagram of the 0.2 kg block,
    T1 = 0.2g + T
    ⇒ T1= 0.2 × 10 + 3 = 5 N
    ∴ The tensions in the two strings are 5 N and 3 N, respectively.
    Page No 79:
  • Qstn #5
    Two blocks of equal mass m are tied to each other through a light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
    Ans :
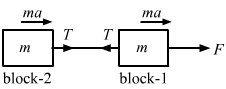
    Let a be the common acceleration of the blocks.
    For block 1,
    `` F-T=ma`` ...(1)
    For block 2,
    T = ma ...(2)
    Subtracting equation (2) from (1), we get:
    `` F-2T=0``
    `` \Rightarrow T=\frac{F}{2}``
    Page No 79:
  • Qstn #6
    A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in figure (5-E1). Find the force acting on the particle at t = 2, 4 and 6 seconds.
    Figure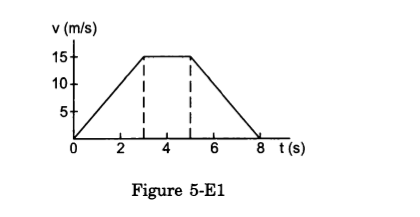
    Ans : Given:
    Mass of the particle, m = 50 g = 5 × 10-2 kg
    Slope of the v-t graph gives acceleration.
    At t = 2 s,
    Slope = `` \frac{15}{3}=5\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    So, acceleration, a = 5 m/s2
    F = ma = 5 × 10-2 × 5
    ⇒ F = 0.25 N along the motion.
    At t = 4 s,
    Slope = 0
    So, acceleration, a = 0
    ⇒ F = 0
    At t = 6 sec,
    Slope = `` \frac{-15}{3}=-5\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    So, acceleration, a = - 5 m/s2
    F = ma = - 5 × 10-2 × 5
    ⇒ F = - 0.25 N along the motion
    or, F = 0.25 N opposite the motion.
    Page No 79:
  • Qstn #7
    Two blocks A and B of mass mA and mB , respectively, are kept in contact on a frictionless table. The experimenter pushes block A from behind, so that the blocks accelerate. If block A exerts force F on block B, what is the force exerted by the experimenter on block A?
    Ans : Let F' = force exerted by the experimenter on block A and F be the force exerted by block A on block B.

    Let a be the acceleration produced in the system.
    For block A,
    `` F\text{ ' }-F={m}_{A}a`` ...(1)
    For block B,
    F = mBa ...(2)
    Dividing equation (1) by (2), we get:
    `` \frac{F\text{ ' }}{F}-1=\frac{{m}_{A}}{{m}_{B}}``
    `` ``
    `` \Rightarrow F\text{ ' }=F\left(1+\frac{{m}_{\,\mathrm{\,A \,}}}{{m}_{\,\mathrm{\,B \,}}}\right)``
    ∴ Force exerted by the experimenter on block A is `` F\left(1+\frac{{m}_{\,\mathrm{\,A \,}}}{{m}_{\,\mathrm{\,B \,}}}\right)``.
    Page No 79:
  • Qstn #8
    Raindrops of radius 1 mm and mass 4 mg are falling with a speed of 30 m/s on the head of a bald person. The drops splash on the head and come to rest. Assuming equivalently that the drops cover a distance equal to their radii on the head, estimate the force exerted by each drop on the head.
    Ans : Given:
    Radius of a raindrop, r = 1 mm = 10-3 m
    Mass of a raindrop, m = 4 mg = 4 × 10-6 kg
    Distance coved by the drop on the head, s = 10-3 m
    Initial speed of the drop, v = 0
    Final speed of the drop, u = 30 m/s
    Using `` a=\frac{{v}^{2}-{u}^{2}}{2s}``, we get:
    `` a=\frac{-{\left(30\right)}^{2}}{2\times {10}^{-3}}=-4.5\times {10}^{5}m/{s}^{2}``
    Force, F = ma
    ⇒ F = 4 × 10-6 × 4.5 × 105
    = 1.8 N
    Page No 79:
  • Qstn #9
    A particle of mass 0.3 kg is subjected to a force F = -kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
    Ans : Displacement of the particle from the mean position, x = 20 cm = 0.2 m
    k = 15 N/m
    Mass of the particle, m = 0.3 kg
    Acceleration, `` a=\frac{\left|\mathit{F}\right|}{m}``
    `` \Rightarrow a=\frac{kx}{m}=\frac{15\left(0.2\right)}{0.3}=\frac{3}{0.3}=10\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    So, the initial acceleration when the particle is released from a point x = 20 cm is 10 m/s2.
    Page No 79:
  • Qstn #10
    Both the springs shown in figure (5-E2) are unstretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
    Figure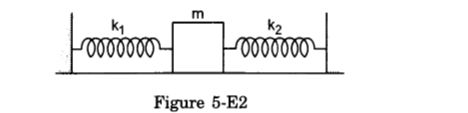
    Ans : Let the block m be displaced towards left by displacement x.

    ∴ F1 = `` -``k1x (compressed)
    F2 = `` -``k2x (expanded)
    `` ma={F}_{1}+{F}_{2}``
    `` \Rightarrow a=\frac{-x\left({k}_{1}+{k}_{2}\right)}{m}``
    i.e. `` \left({k}_{1}+{k}_{2}\right)\frac{x}{m}`` opposite the displacement or towards the mean position.
    Page No 79:
next page