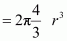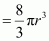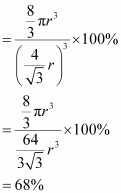NEET-XII-Chemistry
01: The Solid State
- Qstn #6‘Stability of a crystal is reflected in the magnitude of its melting point’. Comment. Collect melting points of solid water, ethyl alcohol, diethyl ether and methane from a data book. What can you say about the intermolecular forces between these molecules?
Ans : Higher the melting point, greater is the intermolecular force of attraction and greater is the stability. A substance with higher melting point is more stable than a substance with lower melting point.
The melting points of the given substances are:
Solid water → 273 K
Ethyl alcohol → 158.8 K
Diethyl ether → 156.85 K
Methane → 89.34 K
Now, on observing the values of the melting points, it can be said that among the given substances, the intermolecular force in solid water is the strongest and that in methane is the weakest.
- Qstn #7How will you distinguish between the following pairs of terms:
Ans :- A 2-D hexagonal close-packing contains two types of triangular voids (a and b) as shown in figure 1. Let us call this 2-D structure as layer A. Now, particles are kept in the voids present in layer A (it can be easily observed from figures 2 and 3 that only one of the voids will be occupied in the process, i.e., either a or b). Let us call the particles or spheres present in the voids of layer A as layer B. Now, two types of voids are present in layer B (c and d). Unlike the voids present in layer A, the two types of voids present in layer B are not similar. Void c is surrounded by 4 spheres and is called the tetrahedral void. Void d is surrounded by 6 spheres and is called the octahedral void.

Figure 1
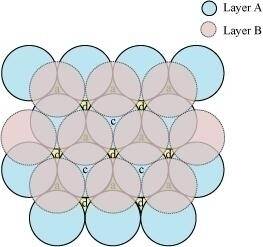

Figure 2
Figure 3
Now, the next layer can be placed over layer B in 2 ways.
Case 1: When the third layer (layer C) is placed over the second one (layer B) in such a manner that the spheres of layer C occupy the tetrahedral voids c.
In this case we get hexagonal close-packing. This is shown in figure 4. In figure 4.1, layer B is present over the voids a and layer C is present over the voids c. In figure 4.2, layer B is present over the voids b and layer C is present over the voids c. It can be observed from the figure that in this arrangement, the spheres present in layer C are present directly above the spheres of layer A. Hence, we can say that the layers in hexagonal close-packing are arranged in an ABAB..... pattern.
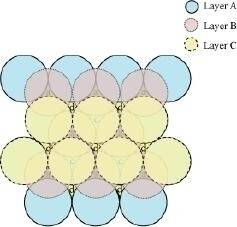
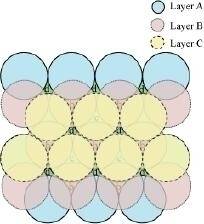
Figure 4.1
Figure 4.2
Case 2: When the third layer (layer C) is placed over layer B in such a manner that the spheres of layer C occupy the octahedral voids d.
In this case we get cubic close-packing. In figure 5.1, layer B is present over the voids a and layer C is present over the voids d. In figure 5.2, layer B is present over the voids b and layer C is present over the voids d. It can be observed from the figure that the arrangement of particles in layer C is completely different from that in layers A or B. When the fourth layer is kept over the third layer, the arrangement of particles in this layer is similar to that in layer A. Hence, we can say that the layers in cubic close-packing are arranged in an ABCABC..... pattern.

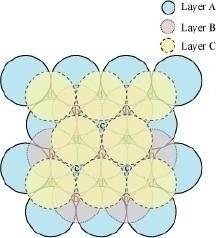
Figure 5.1
Figure 5.2
The side views of hcp and ccp are given in figures 6.1 and 6.2 respectively.
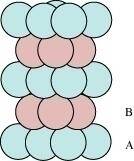
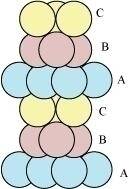
Figure 6.1
Figure 6.2
(ii) The diagrammatic representation of the constituent particles (atoms, ions, or molecules) present in a crystal in a regular three-dimensional arrangement is called crystal lattice.
A unit cell is the smallest three-dimensional portion of a crystal lattice. When repeated again and again in different directions, it generates the entire crystal lattice.
(iii) A void surrounded by 4 spheres is called a tetrahedral void and a void surrounded by 6 spheres is called an octahedral void. Figure 1 represents a tetrahedral void and figure 2 represents an octahedral void.
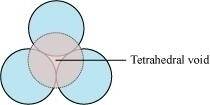
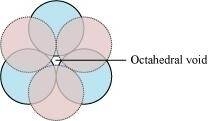
Figure 1
Figure 2
- Qstn #8-iFace-centred cubicAns : There are 14 (8 from the corners + 6 from the faces) lattice points in face-centred cubic.
- Qstn #8-iiFace-centred tetragonalAns : There are 14 (8 from the corners + 6 from the faces) lattice points in face-centred tetragonal.
- Qstn #8-iiiBody-centredAns : There are 9 (1 from the centre + 8 from the corners) lattice points in body-centred cubic.
- Qstn #9-iThe basis of similarities and differences between metallic and ionic crystals.Ans : The basis of similarities between metallic and ionic crystals is that both these crystal types are held by the electrostatic force of attraction. In metallic crystals, the electrostatic force acts between the positive ions and the electrons. In ionic crystals, it acts between the oppositely-charged ions. Hence, both have high melting points.
The basis of differences between metallic and ionic crystals is that in metallic crystals, the electrons are free to move and so, metallic crystals can conduct electricity. However, in ionic crystals, the ions are not free to move. As a result, they cannot conduct electricity. However, in molten state or in aqueous solution, they do conduct electricity.
- Qstn #9-iiIonic solids are hard and brittle.Ans : The constituent particles of ionic crystals are ions. These ions are held together in three-dimensional arrangements by the electrostatic force of attraction. Since the electrostatic force of attraction is very strong, the charged ions are held in fixed positions. This is the reason why ionic crystals are hard and brittle.
- Qstn #10-isimple cubicAns : Simple cubic
In a simple cubic lattice, the particles are located only at the corners of the cube and touch each other along the edge.
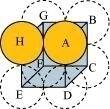
Let the edge length of the cube be ‘a’ and the radius of each particle be r.
So, we can write:
a = 2r
Now, volume of the cubic unit cell = a3
= (2r)3
= 8r3
We know that the number of particles per unit cell is 1.
Therefore, volume of the occupied unit cell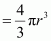
Hence, packing efficiency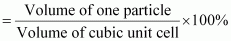
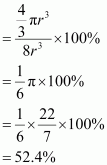
- Qstn #10-iibody-centred cubicAns : Body-centred cubic
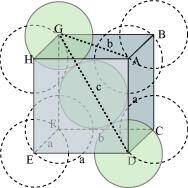
It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.
From ΔFED, we have:
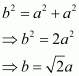
Again, from ΔAFD, we have:
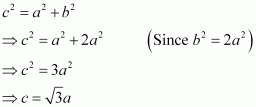
Let the radius of the atom be r.
Length of the body diagonal, c = 4``\pi``
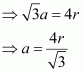
or,
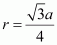
Volume of the cube,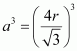
A body-centred cubic lattice contains 2 atoms.
So, volume of the occupied cubic lattice