Qstnid -Ii-10- Calculate The Efficiency Of Packing In Case Of A Metal Crystal For () Simple Cubic () Body-centred Cubic () Face-centred Cubic (With The Assumptions That Atoms Are Touching Each Other). () Body-centred Cubic () Face-centred Cubic (With The Assumptions That Atoms Are Touching Each Other). () Simple Cubic () Body-centred Cubic () Face-centred Cubic (With The Assumptions That Atoms Are Touching Each Other). () Body-centred Cubic () Face-centred Cubic (With The Assumptions That Atoms Are Touching Each Other). - 01: The Solid State

Home Learn Fast select Course

Show Unit/Chapter Change Unit Change Subject Last Menu

NEET-XII-Chemistry

01: The Solid State

page 4

Qstn# II-10 Prvs-Qstn Next-Qstn

#10
Calculate the efficiency of packing in case of a metal crystal for
() simple cubic
() body-centred cubic
() face-centred cubic (with the assumptions that atoms are touching each other).
() body-centred cubic
() face-centred cubic (with the assumptions that atoms are touching each other).
() simple cubic
() body-centred cubic
() face-centred cubic (with the assumptions that atoms are touching each other).
() body-centred cubic
() face-centred cubic (with the assumptions that atoms are touching each other).
Ans : null () Simple cubic

In a simple cubic lattice, the particles are located only at the corners of the cube and touch each other along the edge.

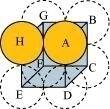
Let the edge length of the cube be ‘a’ and the radius of each particle be r.

So, we can write:

a = 2r

Now, volume of the cubic unit cell = a³

= (2r)³

= 8r³

We know that the number of particles per unit cell is 1.

Therefore, volume of the occupied unit cell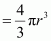

Hence, packing efficiency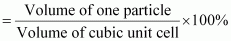

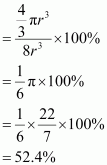
() Body-centred cubic

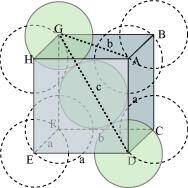
It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.

From ΔFED, we have:

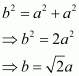
Again, from ΔAFD, we have:

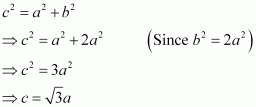
Let the radius of the atom be r.

Length of the body diagonal, c = 4``\pi``

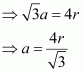
or,

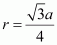
Volume of the cube,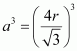

A body-centred cubic lattice contains 2 atoms.

So, volume of the occupied cubic lattice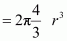

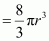
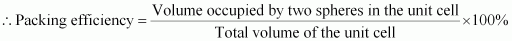
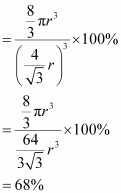
() Face-centred cubic

Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.

From ΔABC, we have:

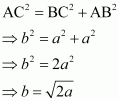
Let r be the radius of the atom.

Now, from the figure, it can be observed that:

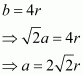
Now, volume of the cube,

We know that the number of atoms per unit cell is 4.

So, volume of the occupied unit cell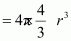

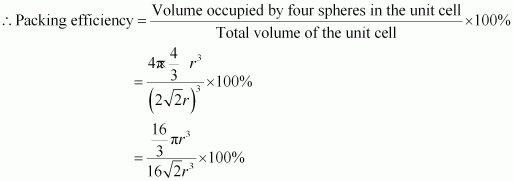
= 74%
() Body-centred cubic

It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.

From ΔFED, we have:

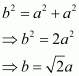
Again, from ΔAFD, we have:

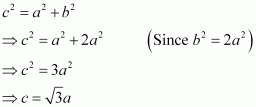
Let the radius of the atom be r.

Length of the body diagonal, c = 4``\pi``

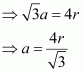
or,

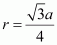
Volume of the cube,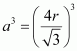

A body-centred cubic lattice contains 2 atoms.

So, volume of the occupied cubic lattice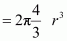

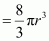
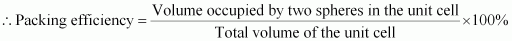
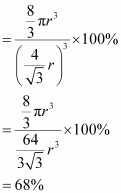
() Face-centred cubic

Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.

From ΔABC, we have:

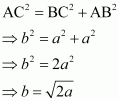
Let r be the radius of the atom.

Now, from the figure, it can be observed that:

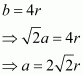
Now, volume of the cube,

We know that the number of atoms per unit cell is 4.

So, volume of the occupied unit cell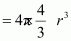

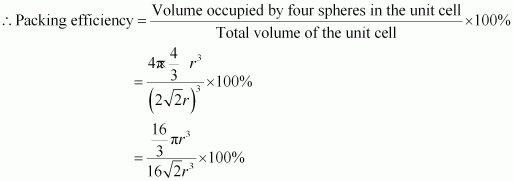
= 74%
() Simple cubic

In a simple cubic lattice, the particles are located only at the corners of the cube and touch each other along the edge.

Let the edge length of the cube be ‘a’ and the radius of each particle be r.

So, we can write:

a = 2r

Now, volume of the cubic unit cell = a³

= (2r)³

= 8r³

We know that the number of particles per unit cell is 1.

Therefore, volume of the occupied unit cell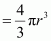

Hence, packing efficiency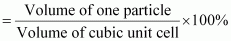

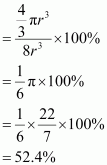
() Body-centred cubic

It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.

From ΔFED, we have:

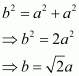
Again, from ΔAFD, we have:

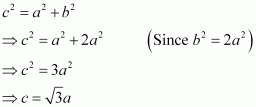
Let the radius of the atom be r.

Length of the body diagonal, c = 4``\pi``

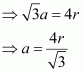
or,

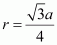
Volume of the cube,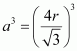

A body-centred cubic lattice contains 2 atoms.

So, volume of the occupied cubic lattice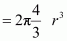

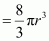
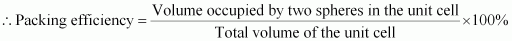
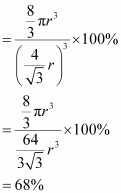
() Face-centred cubic

Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.

From ΔABC, we have:

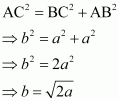
Let r be the radius of the atom.

Now, from the figure, it can be observed that:

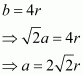
Now, volume of the cube,

We know that the number of atoms per unit cell is 4.

So, volume of the occupied unit cell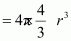

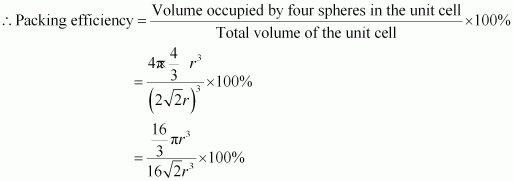
= 74%
() Body-centred cubic

It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.

From ΔFED, we have:

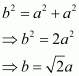
Again, from ΔAFD, we have:

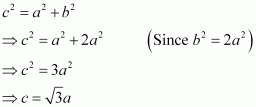
Let the radius of the atom be r.

Length of the body diagonal, c = 4``\pi``

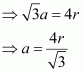
or,

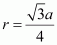
Volume of the cube,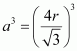

A body-centred cubic lattice contains 2 atoms.

So, volume of the occupied cubic lattice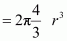

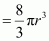
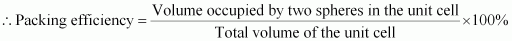
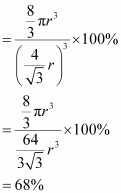
() Face-centred cubic

Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.

From ΔABC, we have:

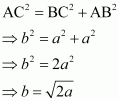
Let r be the radius of the atom.

Now, from the figure, it can be observed that:

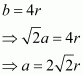
Now, volume of the cube,

We know that the number of atoms per unit cell is 4.

So, volume of the occupied unit cell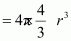

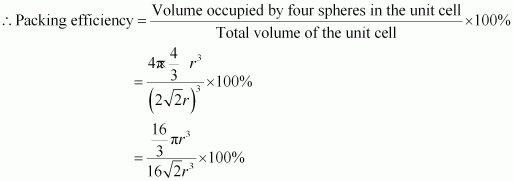
= 74%

#10-i
simple cubic
() body-centred cubic
() face-centred cubic (with the assumptions that atoms are touching each other).
Ans : Simple cubic

In a simple cubic lattice, the particles are located only at the corners of the cube and touch each other along the edge.

Let the edge length of the cube be ‘a’ and the radius of each particle be r.

So, we can write:

a = 2r

Now, volume of the cubic unit cell = a³

= (2r)³

= 8r³

We know that the number of particles per unit cell is 1.

Therefore, volume of the occupied unit cell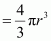

Hence, packing efficiency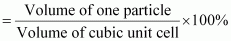

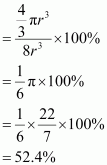
() Body-centred cubic

It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.

From ΔFED, we have:

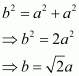
Again, from ΔAFD, we have:

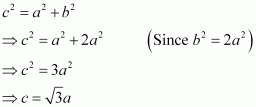
Let the radius of the atom be r.

Length of the body diagonal, c = 4``\pi``

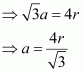
or,

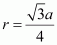
Volume of the cube,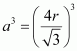

A body-centred cubic lattice contains 2 atoms.

So, volume of the occupied cubic lattice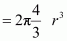

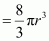
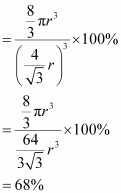
() Face-centred cubic

Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.

From ΔABC, we have:

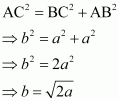
Let r be the radius of the atom.

Now, from the figure, it can be observed that:

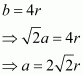
Now, volume of the cube,

We know that the number of atoms per unit cell is 4.

So, volume of the occupied unit cell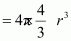

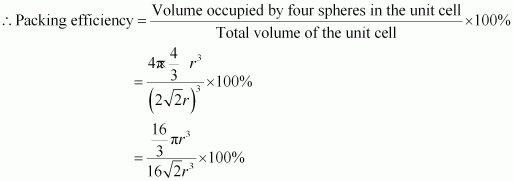
= 74%

#10-ii
body-centred cubic
Ans : Body-centred cubic

It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.

From ΔFED, we have:

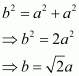
Again, from ΔAFD, we have:

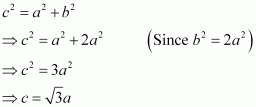
Let the radius of the atom be r.

Length of the body diagonal, c = 4``\pi``

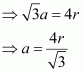
or,

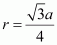
Volume of the cube,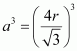

A body-centred cubic lattice contains 2 atoms.

So, volume of the occupied cubic lattice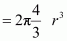

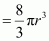
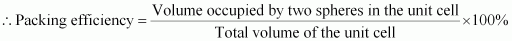
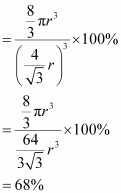
#10-iii
face-centred cubic (with the assumptions that atoms are touching each other).
Ans : Face-centred cubic

Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.

From ΔABC, we have:

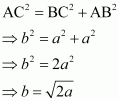
Let r be the radius of the atom.

Now, from the figure, it can be observed that:

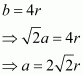
Now, volume of the cube,

We know that the number of atoms per unit cell is 4.

So, volume of the occupied unit cell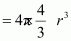

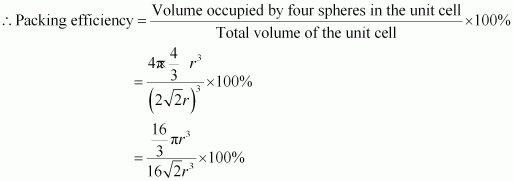
= 74%