NEET-XI-Physics
exam-2 year:2016
- Qstn #120Two rotating bodies A and B of masses m and 2m
with moments of inertia ``I_A`` and ``I_B`` (``I_B`` > ``I_A``) have equal
kinetic energy of rotation. If ``L_A`` and ``L_B`` be their
angular momenta respectively, then :-
(1) ``L_B``> ``L_A``
(2) ``L_A`` > ``L_B``
(3) ``L_A`` = ``L_B``/2
(4) ``L_A`` = 2``L_B``digAnsr: 1Ans : (1)
Sol. KA = KB &implies;
2 2
A B
A B
L L
2I 2I
=
As IB > IA So,
2 2
A BL L &implies;LA < LB
- Qstn #121A solid sphere of mass m and radius R is rotating
about its diameter. A solid cylinder of the same mass
and same radius is also rotating about its geometrical
axis with an angular speed twice that of the sphere.
The ratio of their kinetic energies of rotation
(``E_{sphere}`` / ``E_{cylinder}``) will be :-
(1) 1 : 4
(2) 3 : 1
(3) 2 : 3
(4) 1 : 5digAnsr: 4Ans : (4)
Sol.
Esphere =
2 2 2
s
1 1 2
I MR
2 2 5
=
Ecylinder =
2
2 2
c
1 1 MR
I (2 ) 4
2 2 2
=
sphere
cylinder
E 1
E 5
=
14
- Qstn #122A light rod of length l has two masses ``m_1`` and ``m_2``
attached to its two ends. The moment of inertia of
the system about an axis perpendicular to the rod
and passing through the centre of mass is :-
(1) (``m_1``+ ``m_2``)``l^2 ``
(2)``\sqrt{m_1+ m_2}`` ``l^2``
(3) ``\frac{m_1m_2}{m_1 + m_2}````l^2``
(4) ``\frac{m_1 + m_2}{m_1m_2}````l^2``digAnsr: 3Ans : (3)
Sol.
r1 r2
(CM)m1 m2
2
1
1 2
m
r
m m
=
+
,
1
2
1 2
m
r
m m
=
+
2 2
cm 1 1 2 2I m r m r= +
21 2
1 2
m m
m m
=
+
- Qstn #123Starting from the centre of the earth having radius
R, the variation of g (acceleration due to gravity) is
shown by :-
(1)
(2)
(3)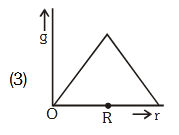
(4) digAnsr: 4Ans : (4)
digAnsr: 4Ans : (4)
Sol. e3
e
GM
g r
R
=
for 0 < r Re &implies; g r
e
2
GM
g
r
= for r ≥ Re &implies; 2
1g
r
- Qstn #124A satellite of mass m is orbiting the earth
(of radius R) at a height h from its surface. The total
energy of the satellite in terms of ``g_0``, the value of
acceleration due to gravity at the earth's surface,is :-
(1)``\frac{2mg_0R^2}{R + h}``
(2) ``-\frac{2mg_0R^2}{R + h}``
(3) ``\frac{mg_0R^2}{2(R + h)}``
(4) ``-\frac{mg_0R^2}{2(R + h)}``digAnsr: 4Ans : (4)
Sol. Total energy = e
GM m
2(R h)
+
2
e 0
0 e2
GM g R
g M
GR
= &implies; =
∴ Energy =
2
0mg R
2(R h)
+
- Qstn #125A rectangular film of liquid is extended from
(4 cm X 2 cm) to (5 cm X 4 cm). If the work done
is 3 X ``10^{-4}`` J, the value of the surface tension of the
liquid is :-
(1) 0.2 ``Nm^{-1}``
(2) 8.0 ``Nm^{-1}``
(3) 0.250 ``Nm^{-1}``
(4) 0.125 ``Nm^{-1}``digAnsr: 4Ans : (4)
Sol. W = T(2▵A) {▵A = (20 - 8) cm2 }
&implies;
W
T
2 A
=
▵
4
1
4
3 10
0.125 Nm
2 12 10
= =
15
- Qstn #126Three liquids of densities ``\rho_1``, ``\rho_2`` and ``\rho_3``
(with ``\rho_1`` > ``\rho_2`` > ``\rho_3``), having the same value of surface
tension T, rise to the same height in three identical
capillaries. The angles of contact ``\theta_1``, ``\theta_2`` and ``\theta_3`` obey:-
(1)``\frac{\pi}{2} < `` ``\theta_1`` < ``\theta_2`` < ``\theta_3`` <``\pi``
(2)``\pi`` > `` ``\theta_1`` > ``\theta_2`` > ``\theta_3`` ``\frac{\pi}{2}``
(3)``\frac{\pi}{2}`` > ``\theta_1`` > ``\theta_2`` > ``\theta_3`` ``\geq 0 ``
(4)0 `` \leq `` ``\theta_1`` < ``\theta_2`` < ``\theta_3`` ``\frac{\pi}{2}``digAnsr: 4Ans : (4)
Sol. h =
2Tcos
gr
As r, h, T are same,
cos
constant
=
&implies;
1 2 3
1 2 3
cos cos cos
= =
As 1 >2 >3
&implies; cos 1 > cos 2 > cos 3 &implies;1 <2 <3
As water rises so must be acute
So, 0 1 < 2 < 3 < /2
- Qstn #127Two identical bodies are made of a material for
which the heat capacity increases with temperature.
One of these is at 100 °C, while the other one is
at 0°C. If the two bodies are brought into contact,
then, assuming no heat loss, the final common
temperature is :-
(1) less than 50 °C but greater than 0 °C
(2) 0 °C
(3) 50 °C
(4) more than 50 °CdigAnsr: 4Ans : (4)
Sol. Let be the final common temperature. Further,
let sc and sh be the average heat capacities of the
cold and hot (initially) bodies respectively (where sc
< sh given)
From, principle of calorimetry,
heat lost = heat gained
sh(100°C - ) = sc
∴ = h
h c c
h
s 100 C
100 C
(s s ) s
1
s
=
+
+
sc / sh < 1 ∴1 + sc / sh < 2
∴>
100 C
or > 50°C
2
- Qstn #128A body cools from a temperature 3T to 2T in
10 minutes. The room temperature is T. Assume
that Newton's law of cooling is applicable. The
temperature of the body at the end of next
10 minutes will be :-
(1)``\frac43`` T
(2) T
(3)``\frac74`` T
(4)``\frac32`` TdigAnsr: 4Ans : (4)
Sol. Newton's laws of cooling
1 2 1 2T T T Tk T
t 2
+
=
3T 2T 5T 2T
k
10 2
=
&implies;
T 3T
k
10 2
=
...(i)
2T T ' 2T T '
k T
10 2
+
=
&implies;
2T T ' T '
k
10 2
=
...(ii)
By solving (i) and (ii)
3
T ' T
2
=
- Qstn #129One mole of an ideal monatomic gas undergoes a
process described by the equation ``PV^3`` = constant.
The heat capacity of the gas during this process is
(1) 2 R
(2) R
(3)``\frac32`` R
(4)``\frac52`` RdigAnsr: 2Ans : (2)
Sol. PVx = constant (Polytropic process)
Heat capacity in polytropic process is given by
V
R
C C
1 x
= +
Given that PV3 = constant &implies; x = 3 ...(1)
also gas is monoatomic so V
3
C R
2
= ...(2)
by formula
3 R 3 R
C R R R
2 1 3 2 2
= + = =
16
- Qstn #130The temperature inside a refrigerator is ``t_2`` °C and
the room temperature is ``t_1``°C. The amount of heat
delivered to the room for each joule of electrical
energy consumed ideally will be :-
(1)``\frac{t_2 + 273}{t_1 - t_2}``
(2) ``\frac{t_1 + t_2}{t_1 + 273}``
(3) ``\frac{t_1 }{t_1 - t_2}``
(4)``\frac{t_1 + 273}{t_1 - t_2}``digAnsr: 4Ans : (4)
Sol. Heat delivered = Q1
COP() =
2 1 1 2
1 2
Q Q W Q T
1
W W W T T
= = =
&implies;
1 2
1 2
Q t 273
1
W t t
+
= +
1
1 2
t 273
t t
+
=
- Qstn #131A given sample of an ideal gas occupies a volume
V at a pressure P and absolute temperature T. The
mass of each molecule of the gas is m. Which of
the following gives the density of the gas ?
(1) P/(kTV)
(2) mkT
(3) P/(kT)
(4) Pm/(kT)digAnsr: 4Ans : (4)
Sol.
w
P RT
M
=
(Ideal gas equation)
&implies;
w A
A
PM P (mN )
RT kN T
= = Pm
kT
=
- Qstn #132A body of mass m is attached to the lower end of
a spring whose upper end is fixed. The spring has
negligible mass. When the mass m is slightly pulled
down and released, it oscillates with a time period
of 3s. When the mass m is increased by 1 kg, the
time period of oscillations becomes 5 s. The value
of m in kg is :-
(1)16/9
(2)9/16
(3)3/4
(4)4/3digAnsr: 2Ans : (2)
Sol.
m
T 2
k
=
m
3 2
k
= ...(1)
m 1
5 2
k
+
= ...(2)
2
2
(1) 9 m 9
m
25 m 1 16(2)
&implies; = &implies; =
- Qstn #133The second overtone of an open organ pipe has the
same frequency as the first overtone of a closed pipe
L metre long. The length of the open pipe will be
(1)``\frac {L}{2}``
(2) 4 L
(3) L
(4) 2 LdigAnsr: 4Ans : (4)
Sol. For second overtone (3rd harmonic) in open organ
pipe,
0
0
3 2
2 3
= &implies; =
for first overtone (3rd harmonic) in closed organ pipe,
C
C
3 4 4L
4 3 3
= &implies; = =
So, 0 0
2 4L
2L
3 3
= &implies; =
- Qstn #134Three sound waves of equal amplitudes have
frequencies (n - 1), n, (n + 1). They superimpose
to give beats. The number of beats produced per
second will be :-
(1) 3
(2) 2
(3) 1
(4) 4digAnsr: 2Ans : (2)
Sol. n-1 n n+1
2
1 1
Now divide 1 second into 1, 1, 2 equal divisions
1
1
1
1
1
2
2
2
By eliminating common time instants, total maxima
in one second is 2.
So, two beats per second will be heard.