Previous Year Paper year:2017 : ICSE-X-Mathematics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2017

with Solutions - page 4

#8-a [3]
Calculate the mean of the following distribution using step deviation method.

Marks 0-10 10-20 20-30 30-40 40-50 50-60
Number of students 10 9 25 30 16 10
Ans : Table as follows:

Marks Mid Term (x) No. of Students (f) D = x-A A = 25 ``t = \frac{x-A}{i} f.t``
0-10 5 10 -20 -2 -20
10-20 15 9 -10 -1 -9
20-30 25 25 0 0 0
30-40 35 30 10 1 30
40-50 45 16 20 2 32
50-60 55 10 30 3 30

``\Sigma f = 100 (``\overline{x}) = A + \frac{ \Sigma ft}{ \Sigma f} \times i = 25 + \frac{63}{100} \times 10 = 25+6.3 = 31.3 ``

#8-b [3]
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of ∠CAQ and
∠PAC. If ∠BAQ = 30o, prove that:
Ans : '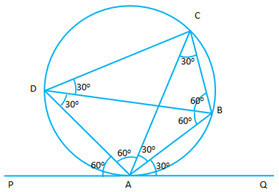
Consider the diagram as shown:
``\angle BAQ = 30 ° `` (Given)
``\angle BAQ = \angle CAB = 30 ° ``
``\therefore \angle CAP = 180 ° -60 ° = 120 ° ``
``\therefore \angle CAD = \angle DAP = 60 ° ``

#8-b-i
BD is a diameter of the circle
Ans : `` \angle DAB = 90 ° ``(since DB is the diameter)

#8-b-ii
ABC is an isosceles triangle

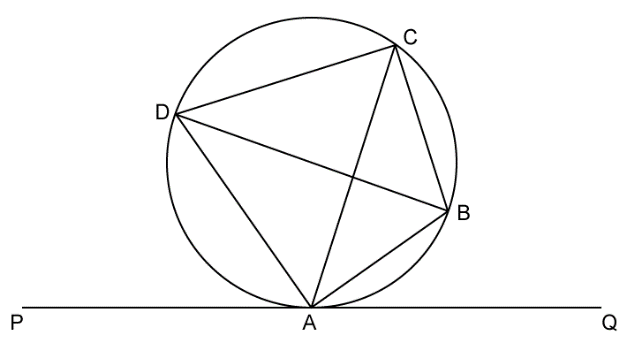Ans : ``\angle CAB = \angle CDB = 30 ° ``(angles subtended by the cord CB on the circumference of the circle)
(iii) ``\angle DAC = \angle DBC = 60 ° `` (angles subtended by the cord DC on the circumference of the circle)
When the chord bisects the tangent.
``\angle DAP = \angle ADC ``
``\therefore \angle ADB = 30 ° ``
``\therefore \angle ABD = 180 ° -90 ° -30 ° =60 ° ``
Also`` \angle DCB = 90 ° ``
``\therefore \angle ACB = 180 ° - 30 ° - 120 ° = 30 ° ``
``\therefore \triangle ACB `` is an isosceles triangle.

#8-c [4]
The printed price of an air conditioner is Rs. 45000/-. The wholesaler allows a discount of 10%
to the shopkeeper. The shopkeeper sells the article to the customer at a discount of 5% of the
marked price. Sales tax (under VAT) is charged at the rate of 12% at every stage. Find:
Ans : Price ``= 45000 \ Rs. ``
Wholesaler to Shopkeeper
Price ``= 45000 \ Rs. ``
Discount ``= 10 \% ``
Therefore discount amount ``= \frac{10}{100} \times 45000 = 4500 \ Rs.``
Therefore discounted price ``= 45000 - 4500 = 40500 \ Rs. ``
VAT ``= 12 \% ``
Therefore VAT paid by the wholesaler`` = \frac{12}{100} \times 40500 = 4860 \ Rs. ``
Shopkeeper to Customer
Price ``= 45000 \ Rs.``
Discount ``= 5 \%``
Therefore discount amount = `` \frac{5}{100} \times 45000 = 2250 \ Rs. ``
Discounted price = 45000 - 2250 = ``42750 \ Rs. ``
VAT = ``12 \% ``
Therefore VAT paid by the retailer = `` \frac{12}{100} \times 42750 = 5130 \ Rs. ``

#8-c-i
VAT paid by the shopkeeper to the government
Ans : VAT paid by the shopkeeper = ``5130 - 4860 = 270 \ Rs. ``

#8-c-ii
The total amount paid by the customer inclusive of tax.
Ans : Total price for the customer = ``42750 + 5130 = 47880 \ Rs. ``

#9
Ans : Answers:

#9-a [3]
In the figure given, O is the centre of the circle. ∠DAE = 70°, Find giving suitable reasons the
measure of: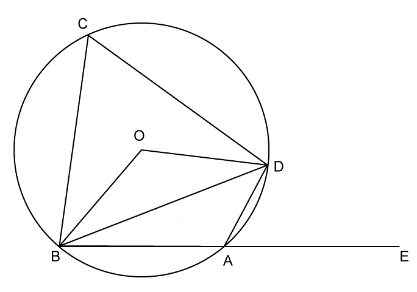

Ans :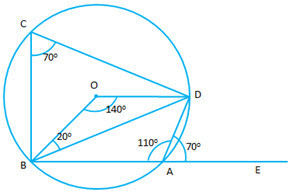
'
`` \angle DAE = 70 ° ``
``\angle DAB = 180 ° -70 ° = 110 ° ``
``\angle BAD + \angle BCD = 180 ° ``
``\angle \Rightarrow BCD = 180 ° - 110 ° = 70 ° ``
``\angle BOD = 2 BCD``
``\angle BOD = 140 ° ``
``\angle OB = OD `` (radius of the same circles)
``\angle \therefore OBD = ODB= x ``
``\angle \therefore 2x = 180 ° - 140 ° \Rightarrow X = 20 ° ``

#9-a-i
∠BCD
Ans : ``\angle BCD = 70 ° `` (ABCD is a cyclic quadrilateral)

#9-a-ii
∠BOD
Ans : `` \angle BOD = 140 ° `` (angle subtended by a chord at the center is twice that subtended on the circumference)

#9-a-iii
∠OBD

Ans :
``\angle OBD = 20 ° ( \triangle OBD`` is isosceles)

#9-b [3]
A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle.
Ans : `` A(-1, 3), B(4, 2) \ and \ C(3, -2)`` are the given coordinates of the three vertices of the triangle

#9-b-i
Find the coordinates of the centroid G of the triangle
Ans : Let the centroid be G(x, y)
Therefore x = `` \frac{-1+3+4}{3} = 2 ``
and y = `` \frac{3-2+2}{3} = 1 ``
Hence centroid is G(2, 1)

#9-b-ii
Find the equation of the line through G and parallel to AC
Ans : Slope of AC = `` \frac{-2-3}{3+1} = \frac{-5}{4} ``
Therefore the slope of the line passing through G and parallel to AC = `` \frac{-5}{4} ``
Hence the equation of the line passing through G and parallel to AC is:
y - 1 = `` \frac{-5}{4} (x-2) ``
``4y - 4 = -5x+10 ``
or`` 4y+5x=14 ``