HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2017

with Solutions - page 5
 
  • #9-c [4]
    Prove that
    $$ \frac{\sin\theta +2\sin^3\theta}{2\cos^3\theta - \cos\theta} = \tan\theta$$
    Ans : ``\frac{sin \ \theta - 2 sin^3 \theta}{2cos^3 \theta - cos \ \theta} = tan \ \theta ``
    LHS = ``\frac{sin \ \theta - 2 sin^3 \theta}{2cos^3 \theta - cos \ \theta} ``
    ``= \frac{sin \ \theta(1 - 2 sin^2 \theta)}{cos \ \theta ( 2cos^2 \theta - 1)} ``
    ``= \frac{sin \ \theta(1 - 2 (1- cos^2 \theta))}{cos \ \theta ( 2cos^2 \theta - 1)} ``
    ``= \frac{sin \ \theta ( 2cos^2 \theta - 1)}{cos \ \theta ( 2cos^2 \theta - 1)} ``
    ``= \frac{sin \ \theta }{cos \ \theta} ``
    ``= tan \theta ``
    = RHS. Hence proved.
  • #10
    Ans : Answers:
  • #10-a [4]
    The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their
    ages in years is 550. Find their ages.
    Ans : Let the age of Vivek = x
    and Let the age of Amit = y
    Given:``x + y = 47 \ and \ xy = 550 ``
    Hence x(47-x) = 550
    ``\Rightarrow X ^2-47x+550=0 ``
    ``\Rightarrow X ^2 -25x-22x+550 = 0 ``
    ``\Rightarrow X (x-25) - 22(x-25) = 0 ``
    ``\Rightarrow(x-22)(x-25) = 0 ``
    ``\Rightarrow X = 22 \ or \ 25 ``
    When x = 22, y = 47-22 = 25
    When x = 25, y = 47-25 = 22
    Hence the age of the two is ``22, \ 25 `` years.
  • #10-b [6]

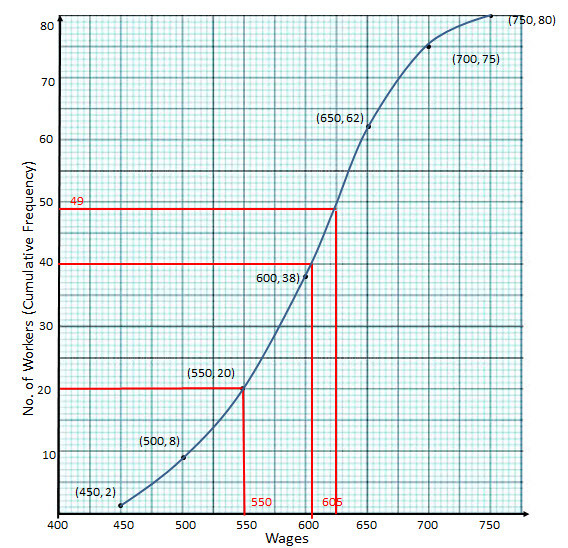
    The daily wages of 80 workers in a project are given below.

    Wages(in Rs.) 400-450 450-500 500-550 550-600 600-650 650-700 700-750
    No. of Workers 2 6 12 18 24 13 5

    Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = Rs.50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate:

    Ans :
    Wages No. workers (f) Cumulative Frequency (c.f)
    400-450 2 2
    450-500 6 8
    500-550 12 20
    550-600 18 38
    600-650 24 62
    650-700 13 75
    700-750 5 80


    On the graph paper, we plot the following points:
    (2, 450), (8, 500), (20, 550), (38,600), (62, 650), (75,700), (80,750)
    '
    n = 80

  • #10-b-i
    the median wage of the workers
    Ans : Median = ``( \frac{n}{2})^{th} `` term = ``\frac{80}{2} =40^{th} ``term
    From the graph ``40^{th} term = 605 ``
  • #10-b-ii
    the lower quartile wage of workers
    Ans : Lower quartile = ``( \frac{n}{4})^{th} \ term = \ \frac{80}{4} =20^{th}`` term
    From the graph ``20^{th}`` term =550
  • #10-b-iii
    the numbers of workers who earn more than Rs. 625 daily
    Ans : The number of workers earning more that 625 per day = 80-49 = 31 students
  • #11
    Ans : Answers:
  • #11-a [3]

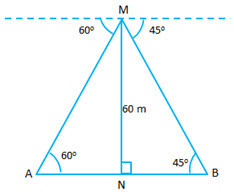
    The angles of depression of two ships A and B as observed from the top of a light house 60 m
    high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house,
    find the distance between the two ships, Give your answer correct to the nearest whole
    number.

    Ans :

    In ``\triangle MNB: tan \ 45 ° = \frac{60}{NB} \Rightarrow NB = 60 \ m ``
    '
    In ``\triangle MNA: tan \ 60 ° = \frac{60}{AN} \Rightarrow AN = \frac{60}{ \sqrt{3}} = 34.64 \ m ``
    Hence AB = NB + NA = 60 + 34.64 = ``94.64 \ m ``
    Rounding off the the nearest whole number, we get AB = ``95 \ m``

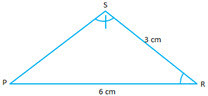
  • #11-b [3]
    PQR is a triangle. S is a point on the side QR of ▲PQR such that ∠PSR = ∠QPR.
    Given QP = 8 cm, PR = 6 cm and SR = 3 cm
    Ans : '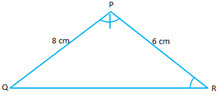
    '
  • #11-b-i
    Prove â–²PQR ``\sim`` â–²SPR
    Ans : Consider ``\triangle PQR`` and ``\triangle PSR``
    ``\angle QPR = \angle PSR`` (given)
    PR is common
    ``\angle R `` is common.
    Therefore by AAA postulate, ``\triangle PQR \sim \triangle PSR``
  • #11-b-ii
    Find the length of QR and PS
    Ans : Since ``\triangle PQR \sim \triangle PSR``
    ``\therefore \frac{PR}{SR} = \frac{QR}{PR}``
    ``\Rightarrow \frac{6}{3} = \frac{QR}{6}``
    ``\Rightarrow QR = 12 \ cm ``
  • #11-b-iii

    $$\frac{\text{area of â–²PQR}}{\text{area of â–²SPR}}$$

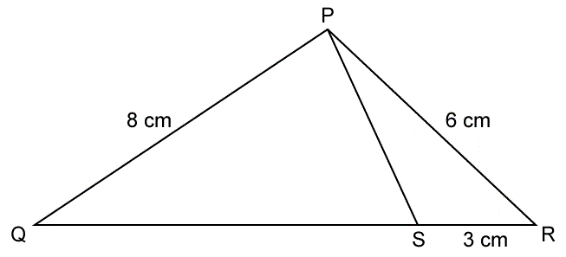    Ans : ``\frac{Area \ of \ \triangle PQR}{Area \ of \ \triangle SPR} = \frac{6^2}{3^2} = \frac{35}{9} = 4:1``
  • #11-c [4]
    Mr. Richard has a recurring deposit account in a bank for 3 years at 7.5% p. a. simple interest. If
    he gets Rs. 8325 as interest at the time of maturity, find
    Ans : I = ``8325 \ Rs.``
    n = ``3 \times 12 = 36 months``
    R = ``7.5 \% ``
  • #11-c-i
    The monthly deposit
    Ans : `` I = \frac{P \times n \times (n+1)}{2} \times \frac{r}{100} \times \frac{1}{12} ``
    ``8325 = \frac{P \times 36 \times 37}{2} \times \frac{7.5}{100} \times \frac{1}{12} ``
    ``\Rightarrow P = \frac{8325 \times 2 \times 100 \times 12}{36 \times 37 \times 7.5} = 2000 \ Rs.``
next page