HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2017

with Solutions - page 3
 
  • #6-a-i
    points equidistant from AB and AC
  • #6-a-ii
    points equidistant from BA and BC
    Hence construct a circle touching the three sides of the triangle internally.
  • #6-b [3]
    A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to
    breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved
    surface area.
    Ans : Radius of the cone ``= 7 \ m ``
    No of people ``= 77 ``
    Volume per person = ``16 \ m^3 ``
    Therefore the volume of the tent =`` 77 \times 16 = 1232 \ m^3 ``
    (i) Volume of the tent = ``\frac{1}{3} \pi r^2 h``
    ``\Rightarrow 1232 = \frac{1}{3} \times \frac{22}{7} \times 7^2 \times h ``
    ``\Rightarrow h = \frac{1232 \times 3}{22 \times 7} = 24 \ m ``
    (ii) Curved surface area of a cone ``= \pi r l ``
    ``l = \sqrt{24^2+7^2} = \sqrt{576 + 49} = 25 ``
    Therefore curved surface area ``= \frac{22}{7} \times 7 \times 25 = 550 \ m^2 ``
  • #6-c [4]
    If ``\frac{7m+2n}{7m-2n} = \frac{5}{3}``, use properties of proportion to find
    Ans : `` \frac{7m+2n}{7m-2n} = \frac{5}{3} ``
  • #6-c-i
    m : n
    Ans : Applying componendo and dividendo
    ``\frac{(7m+2n)+(7m-2n)}{(7m+2n) - (7m-2n)} = \frac{5+3}{5-3}
    \frac{14m}{4n} = \frac{8}{2}
    \frac{7m}{2n} = \frac{4}{1}
    \frac{m}{n} = \frac{8}{7} ``
  • #6-c-ii
    ``\frac{m^2 + n^2}{m^2-n^2}``
    Ans : `` \frac{m^2+n^2}{m^2-n^2}
    = \frac{( \frac{m}{n})^2+1}{( \frac{m}{n})^2-1}
    = \frac{( \frac{8}{7})^2+1}{( \frac{8}{7})^2-1}
    = \frac{64+49}{64-49} = \frac{113}{49} ``
  • #7
    Ans : Answers:
  • #7-a [4]
    A page from a savings bank account passbook is given below:
    DateParticularsAmount withdrawn (Rs.)Amount Deposited (Rs.)Balance(Rs.)
    Jan 7, 2016 B/F 3,000.00
    Jan 10, 2016 By Cheque 2600.00 5600.00
    Feb 8, 2016 To Self 1500.00 4100.00
    Apr 6, 2016 By Cheque2100.00 2000.00
    May 4, 2016 By Cash 6500.00 8500.00
    May 27, 2016 By Cheque 1500.00 10000.00
    Ans : Qualifying principal for various months:
    MonthPrincipal (Rs.)
    January5600
    February4100
    March4100
    April2000
    May8500
    June10000
    Total34300
    P ``= Rs. \ 34300 R = 6 \% \ and \ T= \frac{1}{12} ``
  • #7-a-i
    Calculate the interest for the 6 months from January to June 2016, at 6% per annum.
    Ans : ``I = P \times R \times T = 34300 \times \frac{6}{100} \times \frac{1}{12} = Rs. \ 171.5 ``
  • #7-a-ii
    If the account is closed on 14st July 2016, find the amount received by the account holder.
    Ans : Amount received by the holder on ``1^{st} July = 10000 + 171.5 = 10171.5 \ Rs. ``
  • #7-b [6]
    Use a graph paper for this question (Take 2 cms = 1 unit on both x and y axis)
    Ans : '
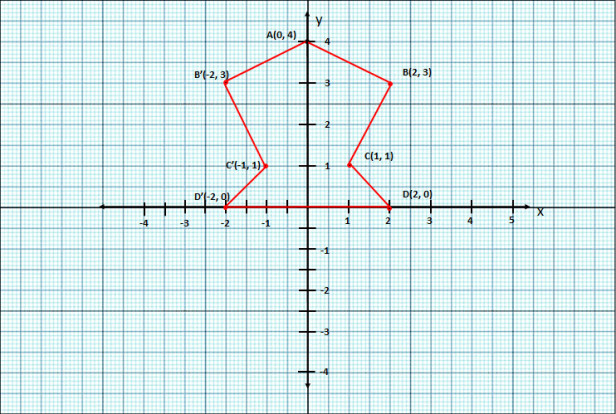  • #7-b-i
    Plot the following points:
    A(0, 4), B(2, 3), C(1, 1) and D(2, 0)
    Ans : Please refer to the diagram above.
  • #7-b-ii
    Reflect points B, C, D on the y-axis and write down their coordinates. Name the
    images as B., C., D. respectively.
    Ans : B'(-2, 3), \ C'(-1, 1) \ and \ D'(-2, 0)
  • #7-b-iii
    Join the points A, B, C, D, D., C., B. and A in order, so as to form a closed figure. Write
    down the equation of the line of symmetry of the figure formed.
    Ans : The enclosed figure is a kite. The line of symmetry is: y = 0 or y-axis
  • #8
    Ans : Answers:
next page