Previous Year Paper year:2017 : ICSE-X-Mathematics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2017

with Solutions - page 2

#3-c [4]
The marks of 10 students of a class in an examination arranged in ascending order is as
follows:
13, 35, 43, x, x + 4, 55, 61, 71, 80
If the median marks is 48, find the value of x. Hence find the mode of the given data.
Ans : 13, 35, 43, 46, x, x+4, 55, 61, 71, 80
Given: Median = 48 and ``n(number \ of \ terms) = 10 ``
Median for even ``n: \frac{ \frac{n^{th}}{2} term + \frac{(n+1)^{th}}{2} term}{2} ``
Hence ``48 = \frac{x+x+4}{2} \Rightarrow 96 = 2x+4 \Rightarrow 2x=92 \Rightarrow x = 46 ``
Hence the ``5^{th} \ term = 46 \ and the \ 6^{th} \ term = 50``
Looking at all the terms, we see that 46 is repeated twice and hence the mode is 46

#4
Ans : Answers:

#4-a [3]
What must be subtracted from ``16x^3 . 8x^2 + 4x + 7`` so that the resulting expression has
2x + 1 as a factor?
Ans : `` f(x) = 16x^3-8x^2+4x+7 ``
Given 2x+1 is a factor ``\Rightarrow 2x+1 = 0 \Rightarrow x = - \frac{1}{2} ``
``f( \frac{-1}{2}) = 16( \frac{-1}{2})^3 -8( \frac{-1}{2})^2 +4( \frac{-1}{2} )+7= -2-2-2+7 = 1 ``
Therefore 1 has to be subtracted from the given polynomial.

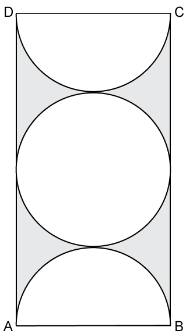
#4-b [3]
In the given figure ABCD is a rectangle. It consists of a circle and two semi-circles each of
which are of radius 5 cm. Find the area of the shaded region. Give your answer correct to
three significant figures.

Ans : '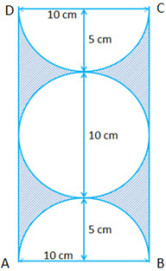
Radius of the circle = ``5 \ cm ``
Therefore, as shown in the diagram: Breadth of the rectangle = ``10 \ cm`` and Length of the rectangle = ``20 \ cm``
Area of ABCD ``= 20 \times 10 = 200 \ cm^2 ``
Taking ``\pi = 3.14 ``
Area of the circles and semi circles ``= 2 \times \pi r^2 = 2 \times 3.14 \times 5^2 = 157 \ cm^2 ``
Therefore the shaded area =`` 200 = 157 = 43 \ cm^2 ``

#4-c [4]
Solve the following inequation and represent the solution set on a number line.
$$-8\frac12 \lt -\frac12 - 4x \le 7\frac12 , x\epsilon 1 $$
Ans : Given ``-8 \frac{1}{2} < - \frac{1}{2}-4x \leq 7 \frac{1}{2} ``
``\Rightarrow - \frac{17}{2} < \frac{-1-8x}{2} \leq \frac{15}{2} ``
``\Rightarrow -17 < -1-8 \leq 15 ``
Therefore we have two equations:
``-17 < -1-8x ``
``\Rightarrow 17 > 1+8x ``
``\Rightarrow 8x < 16 ``
``\Rightarrow x < 2 ``
``-1-8x \leq 15 ``
``\Rightarrow 1+8x \geq -15 ``
``\Rightarrow 8x \geq -16 ``
``\Rightarrow x \geq -2 ``
Hence ``-2 \leq x < 2 ``
Since ``x \in I`` , the values of ``x \ are \ -2, -1, 0, 1 ``

# [40]
Section : B
Attempt any four questions from this section

#5
Ans : Answers:

#5-a [3]
21 1Given matrix B =\begin{bmatrix} 1 & 1\\ 8 & 3 \\ \end{bmatrix}, find the matrix X if, ``X = B^2 - 4B``.
Hence solve for a and b given ``X \cdot \begin{bmatrix} a \\b\\ \end{bmatrix} = \begin{bmatrix} 5 \\ 50\\ \end{bmatrix}`` .
Ans : X ``= B^2-4B ``
``\Rightarrow X = \begin{bmatrix} 1 & 1 \ \ 8 & 3 \end{bmatrix} \times \begin{bmatrix} 1 & 1 \ \ 8 & 3 \end{bmatrix} - 4 \times \begin{bmatrix} 1 & 1 \ \ 8 & 3 \end{bmatrix} ``
``\Rightarrow X = \begin{bmatrix} 1+8 & 1+3 \ \ 8+24 & 8+9 \end{bmatrix} - \begin{bmatrix} 4 & 4 \ \ 32 & 12 \end{bmatrix} ``
``\Rightarrow X = \begin{bmatrix} 9 & 4 \ \ 32 & 17 \end{bmatrix} - \begin{bmatrix} 1 & 1 \ \ 8 & 3 \end{bmatrix} ``
``\Rightarrow X = \begin{bmatrix} 5 & 0 \ \ 0 & 5 \end{bmatrix} ``
Now X \begin{bmatrix} a \ \ b \end{bmatrix} = \begin{bmatrix} 5 \ \ 50 \end{bmatrix}
``\Rightarrow \begin{bmatrix} 5 & 0 \ \ 0 & 5 \end{bmatrix} \times \begin{bmatrix} a \ \ b \end{bmatrix} = \begin{bmatrix} 5 \ \ 50 \end{bmatrix} ``
``\Rightarrow \begin{bmatrix} 5a \ \ 5b \end{bmatrix} = \begin{bmatrix} 5 \ \ 50 \end{bmatrix} ``
``\Rightarrow a = 1 \ and \ b = 10 ``

#5-b [3]
How much should a man invest in Rs. 50 shares selling at Rs. 60 to obtain an income of
Rs. 450, if the rate of dividend declared is 10%. Also find his yield percent, to the nearest
whole number.
Ans : Face Value (FV) = ``50 \ Rs. ``
Market Value (MV) = ``60 \ Rs. ``
Dividend = ``10 \% ``
(i) Let the number of shares bought = n
Dividend Amount ``= FV \times (no. \ of \ shares) \times Dividend \% ``
``\Rightarrow 450 = 50 \times n \times \frac{10}{100} ``
``\Rightarrow n =90 ``
(ii) Profit ``= 450 \ Rs., \ n = 90 \ MV = 60 \ Rs. ``
Investment ``= 90 \times 60 = 5400 \ Rs. ``
Yield ``\% = \frac{450}{5400} \times 100 = 8.33 \% ``
Therefore yield nearest to a whole number is`` 8 \%``

#5-c [4]
Sixteen cards are labeled as a, b, c, ...... m, n, o, p. They are put in a box and shuffled. A
boy is asked to draw a card from the box. What is the probability that the card drawn is:
Ans : No of cards = 16
Cards: a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
(i) No of vowels: a, e, i, o
Probability (vowels) = ``\frac{4}{16} = 0.25 ``
(ii) No of consonants: b, c, d, f, g, h, j, k, l , m, n, p
Probability (consonants) = ``\frac{12}{16} = 0.75 ``
(iii) Letters other than .median. = b, c, f, g, h, j, k, l, o, p
Probability (other than median) = ``\frac{10}{16} = \frac{5}{8} = 0.625 ``

#5-c-a
a vowel

#5-c-b
a consonant

#5-c-c
none of the letters of the word median

#6
Ans : Answers:

#6-a [3]
Using a ruler and a compass construct a triangle ABC in which AB = 7 cm, ∠CAB = 60° and
AC = 5 cm. Construct the locus of
Ans :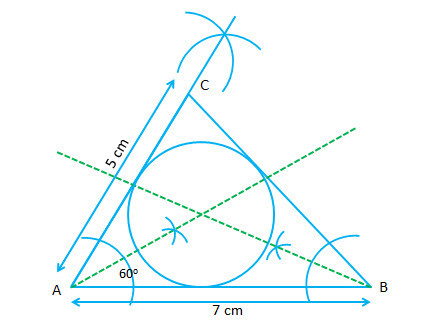 '