Previous Year Paper year:2018 : ICSE-X-Mathematics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2018

with Solutions - page 2

#2-c [4]
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°,
calculate: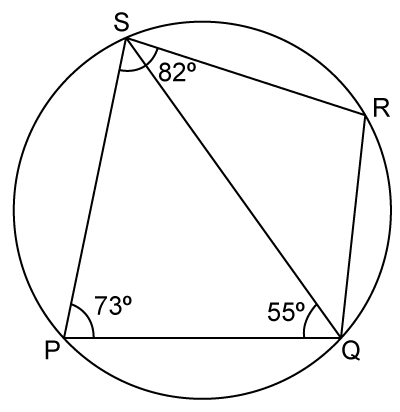

Ans :
Join PR

#2-c-i
∠QRS
Ans : ``\angle SPQ + \angle QRS = 180° ``
'
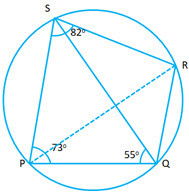``\Rightarrow \angle QRS = 180° - 73° = 107°`` (opposite angles of a cyclic quadrilateral)

#2-c-ii
∠RQS
Ans : ``\angle PSR + \angle PQR = 180°``
``\Rightarrow 82°+55°+\angle SQR = 180°``
``\Rightarrow \angle SQR = 180° -82°-55° = 43°``

#2-c-iii
∠PRQ

Ans :
``\angle PSR = 55° = \angle PQS ``(angles in the same segment)
``\therefore \angle SRQ = 180° - 73° = 107°``
``\angle PRQ = 105° - 55° = 52° ``

#3

#3-a [3]
If (x + 2) and (x + 3) are factors of ``x^3 + ax + b``, find the values of 'a' and `b'.
Ans : ``f(x) = x^3+ax+b``
Factors: x+2 = 0 ``\Rightarrow x = -2``
x+3 = 0 ``\Rightarrow x = -3``
``f(-2) = (-2)^3+a(-2)+b =0``
``\Rightarrow 2a-b = -8`` . . . . . (i)
``f(-3) = (-3)^3+a(-3)+b =0``
``\Rightarrow -3a+b = 27 `` . . . . . (ii)
Solving (i) and (ii)
``2a-b=-8 \\ \underline{-3a+b=27} \\ -a \ \ \ \ \ \ \ = 19``
``\Rightarrow a = -19``
Substituting in (ii)
2(-19)-b = -8
``\Rightarrow b = -30``

#3-b [3]
Prove that
$$ \sqrt{\sec^2\theta + cosec^2\theta} = \tan\theta + \cot\theta $$
Ans : ``\sqrt{sec^2 \theta + csec^2 \theta} = tan \ \theta + cot \ \theta``
``LHS = \sqrt{sec^2 \theta + csec^2 \theta}``
``= \sqrt{1+tan^2 \theta + 1 + cot^2 \theta}``
``= \sqrt{2+tan^2 \theta + cot^2 \theta}``
``= \sqrt{2 tan \ \theta cot \ \theta+tan^2 \theta + cot^2 \theta}``
``=\sqrt{(tan \ \theta + cot \ \theta)^2}``
``= tan \ \theta + cot \ \theta``
= RHS . Hence proved.

#3-c [4]
Using a graph paper draw a histogram for the given distribution showing the
number of runs scored by 50 batsmen. Estimate the mode of the data:

Runs scored 3000-4000 4000-5000 5000-6000 6000-7000 7000-8000 8000-9000 9000-10000

No. of batsmen 4 18 9 6 7 2 4

Ans : '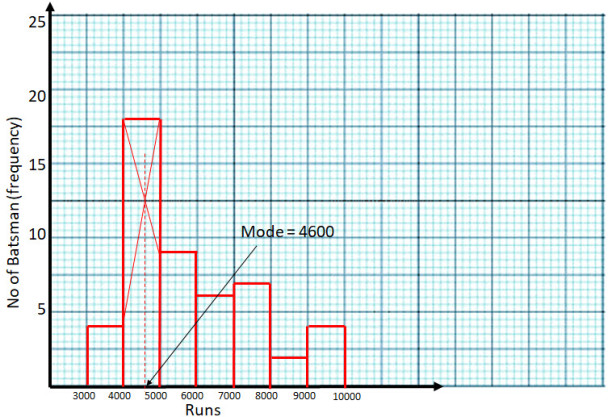
Mode = 4600

#4
Ans : Answers:

#4-a [3]
Solve the following inequation, write down the solution set and represent it on the
real number line:
``-2 + 10x \le 13x +10 \lt 24 +10x`` , ``x \, \epsilon \, Z``
Ans : ``-2+10x \leq 13x + 10 \leq 24 + 10x, x \in Z``
First equation: ``-2+10x \leq 13x + 10``
``\Rightarrow -12 \leq 3x``
``\Rightarrow -4 \leq x``
Second equation: ``13x + 10 \leq 24 + 10x``
``\Rightarrow 3x < 14``
``\Rightarrow x < \frac{14}{3} ``
``\therefore -4 \leq x < \frac{14}{3} ``
Hence the solution set ``= \{x \in Z: -4, -3, -2, -1, 0, 1, 2, 3, 4 \}``

#4-b [3]
If the straight lines ``3x - 5y = 7 ``and ``4x + ay + 9 = 0`` are perpendicular to one another,
find the value of a.
Ans : Two equations are:
``3x-5y=7 \Rightarrow y = \frac{3}{5} x - \frac{7}{5} \Rightarrow m_1 = \frac{3}{5}``
``4x+ay+9=0 \Rightarrow y = \frac{-4}{a} x - \frac{1}{a} \Rightarrow m_2 = \frac{-4}{a}``
Since the two lines are perpendicular to each other
``m_1 \times m_2 = -1\frac{3}{5} \times \frac{-4}{a} = -1 \Rightarrow a = \frac{12}{5}``

#4-c [4]
Solve ``x^2 + 7x = 7`` and give your answer correct to two decimal places.
Ans : ``x^2+7x=7``
``x^2+7x-7=0``
``\Rightarrow a = 1, b = 7, c = -7``
``x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}``
``= \frac{-7 \pm \sqrt{7^2+4.1.17}}{2.1}``
``= \frac{-7 \pm \sqrt{77}}{2}``
``= \frac{-7 \pm 8.77}{2}``
Therefore ``x = \frac{-7 + 8.77}{2.1}, \frac{-7 - 8.77}{2}``
or ``x = 0.885 \approx 0.89, -7.885 \approx 7.89``

# [40]
Section : B
Attempt any four questions from this Section

#5

#5-a [3]
The 4^th term of a G.P. is 16 and the 7^th term is 128. Find the first term and common ratio of the series.
Ans : ``4^{th} \ term = 16, \ 7^{th} \ term = 128``
``T_n = ar^{n-1}``
Therefore ``T_4: 16 = ar^3 \Rightarrow \frac{16}{a} =r^3``
``T_7: 128 = ar^6``
``\Rightarrow 128 = a(r^3)^2``
``\Rightarrow 128 = a. (\frac{16}{a})^2``
``\Rightarrow 128 = a . \frac{16^2}{a^2} ``
``\Rightarrow a = \frac{256}{128} = 2``
Therefore ``r^3 = \frac{16}{2} = 8 \Rightarrow r = 2``