22: Photometry : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

22: Photometry

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#3-a
480 nm,
Ans : The relative luminosity of wavelength 480 nm is 0.14.

#3-b
520 nm
Ans : The relative luminosity of wavelength 520 nm is 0.68.

#3-c
580 nm and
Ans : The relative luminosity of wavelength 580 nm is 0.92.

#3-d
600 nm.
Ans : The relative luminosity of wavelength 600 nm is 0.66.
Page No 455:

Qstn #4
The relative luminosity of wavelength 600 nm is 0.6. Find the radiant flux of 600 nm needed to produce the same brightness sensation as produced by 120 W of radiant flux at 555 nm.
Ans : Given,
Relative luminosity = 0.6
Let P be the radiant flux of the source.
∴ Luminous flux = P`` \times ``685
Again, relative luminosity`` =\frac{\,\mathrm{\,Luminous\,}\,\mathrm{\,flux\,}\,\mathrm{\,of\,}\,\mathrm{\,a\,}\,\mathrm{\,source\,}\,\mathrm{\,of\,}\,\mathrm{\,given\,}\,\mathrm{\,wavelength\,}}{\,\mathrm{\,Luminous\,}\,\mathrm{\,flux\,}\,\mathrm{\,of\,}\,\mathrm{\,a\,}\,\mathrm{\,source\,}\,\mathrm{\,of\,}555\,\mathrm{\,nm\,}\,\mathrm{\,of\,}\,\mathrm{\,same\,}\,\mathrm{\,power\,}}``
`` ``
`` \therefore 0.6=\frac{\,\mathrm{\,Luminous\,}\,\mathrm{\,flux\,}\,\mathrm{\,of\,}\,\mathrm{\,a\,}\,\mathrm{\,source\,}P\,\mathrm{\,watt\,}}{685P}``
`` \Rightarrow 685\times P\times 0.6=120\times 685``
`` \Rightarrow \,\mathrm{\,P\,}=\frac{120}{0.6}=200\,\mathrm{\,W\,}``
So, 200 W radiant flux is needed to produce the same brightness sensation for 600 nm wavelength.
Page No 455:

Qstn #5
The luminous flux of a monochromatic source of 1 W is 450 lumen watt^-1. Find the relative luminosity at the wavelength emitted.
Ans :
Given,
The luminous flux of the given source is 450 lumen/watt.
`` \,\mathrm{\,We\,}\,\mathrm{\,know\,}that\,\mathrm{\,luminous\,}\,\mathrm{\,flux\,}\,\mathrm{\,of\,}555\,\mathrm{\,nm\,}\,\mathrm{\,source\,}\,\mathrm{\,of\,}1W=685\,\mathrm{\,lum\,}ens``
∴ Relative luminosity is given by,
`` \frac{\,\mathrm{\,Luminous\,}\,\mathrm{\,flux\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,source\,}\,\mathrm{\,of\,}\,\mathrm{\,given\,}\,\mathrm{\,wavelength\,}}{\,\mathrm{\,Luminous\,}\,\mathrm{\,flux\,}\,\mathrm{\,of\,}555\,\mathrm{\,nm\,}\,\mathrm{\,source\,}\,\mathrm{\,of\,}\,\mathrm{\,same\,}\,\mathrm{\,power\,}}=\frac{450}{685}=66\%``
So, the relative luminosity at the wavelength emitted is 66 %.
Page No 455:

Qstn #6
A source emits light of wavelengths 555 nm and 600 nm. The radiant flux of the 555 nm part is 40 W and of the 600 nm part is 30 W. The relative luminosity at 600 nm is 0.6. Find
Ans : Given,
The radiant flux of the light of wavelength 555 nm is 40 W.
The radiant flux of the light of wavelength 600 nm is 30 W.
The relative luminosity at 600 nm is 0.6.

#6-a
the total radiant flux,
Ans : Total radiant flux = radiant flux of 555 nm part of light + radiant flux of 600 nm part of light
= 40 W + 30 W = 70 W

#6-b
the total luminous flux,
Ans : Total luminous flux = luminous flux of 555 nm part of light + luminous flux of 600 nm part of light
= 1 × 40 × 685 + 0.6 × 30 × 685
= 39730 lumen

#6-c
the luminous efficiency.
Ans : `` \,\mathrm{\,Luminous\,}\,\mathrm{\,efficiency\,}=\frac{\,\mathrm{\,Total\,}\,\mathrm{\,luminous\,}\,\mathrm{\,flux\,}}{\,\mathrm{\,Total\,}\,\mathrm{\,radiant\,}\,\mathrm{\,flux\,}}``
`` =\frac{39730}{70}=567.6\,\mathrm{\,lumen\,}/\,\mathrm{\,W\,}``
So, the luminous efficiency is 568 lumen/W.
Page No 455:

Qstn #7
A light source emits monochromatic light of 555 nwavelengthm. The source consumes 100 W of electric power and emits 35 W of radiant flux. Calculate the overall luminous efficiency.
Ans : Given:
Wavelength of light, `` \lambda `` = 555 nm
Radiant flux emitted = 35 W
Power input = 100 W
Overall luminous efficiency = `` \frac{\,\mathrm{\,Total\,}\,\mathrm{\,luminous\,}flux}{\,\mathrm{\,Power\,}input}=\frac{35\times 685}{100}=239.75\,\mathrm{\,lm\,}/\,\mathrm{\,W\,}``
So, the overall luminous efficiency will be 240 lm/W.
Page No 455:

Qstn #8
A source emits 31.4 W of radiant flux distributed uniformly in all directions. The luminous efficiency is 60 lumen watt^-1. What is the luminous intensity of the source?
Ans : Given that,
Radiant flux = 31.4 W
Since the radiant flux is distributed uniformly in all directions, the solid angle will be 4`` \,\mathrm{\,\pi \,}``
Luminous efficiency = 60 lumen/W
So, luminous flux = luminous efficiency `` \times `` radiant flux
= 60 × 31.4 lumen
Luminous intensity = `` \frac{\,\mathrm{\,Luminous\,}\,\mathrm{\,Flux\,}}{\,\mathrm{\,Solid\,}\,\mathrm{\,angle\,}}=\frac{\,\mathrm{\,Luminous\,}\,\mathrm{\,Flux\,}}{4\,\mathrm{\,\pi \,}}``
`` =\frac{60\times (31.4)}{4\,\mathrm{\,\pi \,}}``
`` =150\,\mathrm{\,candela\,}``
Page No 455:

Qstn #9
A point source emitting 628 lumen of luminous flux uniformly in all directions is placed at the origin. Calculate the illuminance on a small area placed at (1.0 m, 0, 0) in such a way that the normal to the area makes an angle of 37° with the X-axis.
Ans : Given,
Luminous flux = 628 lumen
Angle made by the normal with the x axis (`` \theta ``) = 37^ₒ
Distance of point, r = 1 m
Since the radiant flux is distributed uniformly in all directions, the solid angle will be 4`` \,\mathrm{\,\pi \,}``.
∴ Luminous intensity, l =`` \frac{\,\mathrm{\,Luminous\,}\,\mathrm{\,Flux\,}}{\,\mathrm{\,Solid\,}\,\mathrm{\,angle\,}}``
`` ``
`` =\frac{628}{4\,\mathrm{\,\pi \,}}=50\,\mathrm{\,candela\,}``
`` ``
`` I\,\mathrm{\,lluminance\,}\left(E\right)\,\mathrm{\,is\,}\,\mathrm{\,given\,}\,\mathrm{\,by\,},``
`` E=l\,\mathrm{\,cos\,}\frac{\theta }{{r}^{2}}``
On substituting the respective values we get,
`` E=50\times \frac{\,\mathrm{\,cos\,}37°}{{1}^{2}}``
`` =50\times \frac{(4/5)}{1}=40\,\mathrm{\,lux\,}``
So, the illuminance on the area is 40 lux.
Page No 455:

Qstn #10
The illuminance of a small area changes from 900 lumen m^-2 to 400 lumen m^-2 when it is shifted along its normal by 10 cm. Assuming that it is illuminated by a point source placed on the normal, find the distance between the source and the area in the original position.
Ans : Let the luminous intensity of the source be l and the distance between the source and the area, in the initial position, be x.
Given,
Initial illuminance (E_A) = 900 lumen/m²
Final illuminance (E_B) = 400 lumen/m²
Illuminance on the initial position is given by,
`` {E}_{\,\mathrm{\,A\,}}=l\frac{\,\mathrm{\,cos\,}\theta }{{x}^{2}}`` ......(1)
Illuminance at final position is given by
`` {E}_{\,\mathrm{\,B\,}}=\frac{l\,\mathrm{\,cos\,}\theta }{(x+10{)}^{2}}``.......(2)
Equating luminous intensity from `` \left(1\right)`` and `` \left(2\right)``, we get
`` l=\frac{{E}_{\,\mathrm{\,A\,}}{x}^{2}}{\,\mathrm{\,cos\,}\theta }=\frac{{E}_{B}(x+10{)}^{2}}{\,\mathrm{\,cos\,}\theta }``
`` ``
`` \Rightarrow 900{x}^{2}=400(x+10{)}^{2}``
`` \Rightarrow \frac{x}{x+10}=\frac{2}{3}``
⇒ 3x = 2x + 20
`` \Rightarrow `` x = 20 cm
The distance between the source and the area at the initial phase was 20 cm.
Page No 455:

Qstn #11
A point source emitting light uniformly in all directions is placed 60 cm above a table-top. The illuminance at a point on the table-top, directly below the source, is 15 lux. Find the illuminance at a point on the table-top 80 cm away from the first point.
Ans : Given,
Distance of the source from the table-top (r) = 60 cm or 0.6 m
Let I_obe the intensity of illumination.
Illuminance directly below the source `` \left({E}_{A}\right)`` is given by,
`` {E}_{A}=\frac{{I}_{0}}{(0.6{)}^{2}}``
⇒ I₀ = 15 × (0.6)²
= 5.4 candela

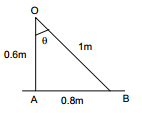
Let E_B be the illuminance at a point 80 cm away from the initial point.
So, `` {E}_{B}=\frac{{I}_{0}\,\mathrm{\,cos\,}\theta }{{\left(OB\right)}^{2}}``
From the figure, we get
cos`` \theta `` = `` \frac{0.6}{1}``
OB = 1 m
Substituting the respective values in the above formula, we get
E_B `` =5.4\left(\frac{0.6}{1}\right)``
`` =3.24\,\mathrm{\,lux\,}``
So, the illuminance at a point on the table-top 80 cm away from the first point is 3.24 lux.
Page No 455: