NEET-XII-Physics
22: Photometry
- #11A point source emitting light uniformly in all directions is placed 60 cm above a table-top. The illuminance at a point on the table-top, directly below the source, is 15 lux. Find the illuminance at a point on the table-top 80 cm away from the first point.Ans : Given,
Distance of the source from the table-top (r) = 60 cm or 0.6 m
Let Io be the intensity of illumination.
Illuminance directly below the source `` \left({E}_{A}\right)`` is given by,
`` {E}_{A}=\frac{{I}_{0}}{(0.6{)}^{2}}``
⇒ I0 = 15 × (0.6)2
= 5.4 candela
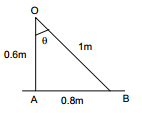
Let EB be the illuminance at a point 80 cm away from the initial point.
So, `` {E}_{B}=\frac{{I}_{0}\,\mathrm{\,cos\,}\theta }{{\left(OB\right)}^{2}}``
From the figure, we get
cos`` \theta `` = `` \frac{0.6}{1}``
OB = 1 m
Substituting the respective values in the above formula, we get
EB `` =5.4\left(\frac{0.6}{1}\right)``
`` =3.24\,\mathrm{\,lux\,}``
So, the illuminance at a point on the table-top 80 cm away from the first point is 3.24 lux.
Page No 455: