NEET-XII-Physics
22: Photometry
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #6A battery-operated torch is adjusted to send an almost parallel beam of light. It produces an illuminancle of 40 lux when the light falls on a wall 2 m away. The illuminance produced when it falls on a wall 4 m away is close to
(a) 40 lux
(b) 20 lux
(c) 10 lux
(d) 5 luxdigAnsr: aAns : Correct option
(a)
Since the beam is parallel, it will have no angular spread. So the illuminance will remain same throughout. Therefore, in this case, it will be 40 lux.
Page No 454:
- Qstn #7The intensity produced by a long cylindrical light source at a small distance r from the source is proportional to
(a)``1r^2``
(b)``1r^3``
(c)1r
(d) none of thesedigAnsr: CAns : Correct option
(c).
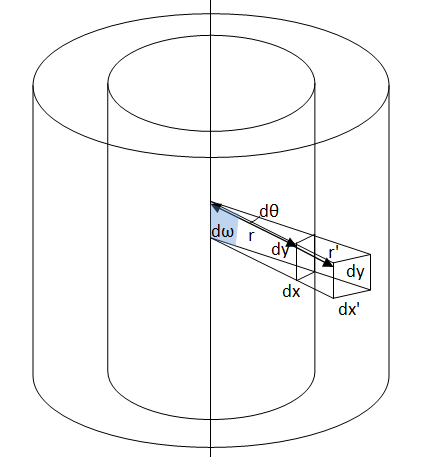
Let us consider two coaxial cylindrical surfaces at distances r and r' from the axis. Let areas dA and dA' subtend the solid angle dω at the central axis. The height of the area element will be same, i.e. equal to dy. Let the breath of dA be dx and that of dA' be dx'.
`` \,\mathrm{\,Now\,}\,\mathrm{\,from\,}\,\mathrm{\,the\,}\,\mathrm{\,arc\,}s,``
`` \,\mathrm{\,dx\,}=\,\mathrm{\,rd\theta \,}``
`` \,\mathrm{\,dx\,}\text{'}=\,\mathrm{\,r\,}\text{'}\,\mathrm{\,d\theta \,}``
`` \,\mathrm{\,Now\,},``
`` \,\mathrm{\,dA\,}=\,\mathrm{\,dxdy\,}=\,\mathrm{\,rd\theta dy\,}``
`` \,\mathrm{\,dA\,}\text{'}=\,\mathrm{\,dx\,}\text{'}\,\mathrm{\,dy\,}=\,\mathrm{\,r\,}\text{'}\,\mathrm{\,d\theta dy\,}``
`` \frac{\,\mathrm{\,dA\,}}{\,\mathrm{\,dA\,}\text{'}}=\frac{\,\mathrm{\,r\,}}{\,\mathrm{\,r\,}\text{'}}``
`` \Rightarrow \frac{\,\mathrm{\,dA\,}}{\,\mathrm{\,r\,}}=\frac{\,\mathrm{\,dA\,}\text{'}}{\,\mathrm{\,r\,}\text{'}}=\,\mathrm{\,d\omega \,}``
`` ``
The luminous flux going through the solid angle dω will be:
dF = Idω
`` \,\mathrm{\,Now\,},``
`` \,\mathrm{\,dF\,}=\,\mathrm{\,I\,}\frac{\,\mathrm{\,dA\,}}{\,\mathrm{\,r\,}}``
`` \,\mathrm{\,If\,}\,\mathrm{\,the\,}\,\mathrm{\,surfaces\,}\,\mathrm{\,are\,}\,\mathrm{\,inclined\,}\,\mathrm{\,at\,}\,\mathrm{\,an\,}\,\mathrm{\,angle\,}\,\mathrm{\,\alpha \,},``
`` \,\mathrm{\,dF\,}=\,\mathrm{\,I\,}\frac{\,\mathrm{\,dAcos\alpha \,}}{\,\mathrm{\,r\,}}``
`` \,\mathrm{\,Now\,},\,\mathrm{\,illuminance\,}\,\mathrm{\,is\,}\,\mathrm{\,defined\,}\,\mathrm{\,as\,}``
`` \,\mathrm{\,E\,}=\frac{\,\mathrm{\,dF\,}}{\,\mathrm{\,dA\,}}=\,\mathrm{\,I\,}\frac{\,\mathrm{\,dAcos\alpha \,}}{\,\mathrm{\,r\,}}``
`` \Rightarrow \,\mathrm{\,E\,}\propto \frac{1}{\,\mathrm{\,r\,}}``
`` ``
Page No 454:
- Qstn #8A photographic plate placed a distance of 5 cm from a weak point source is exposed for 3 s. If the plate is kept at a distance of 10 cm from the source, the time needed for the same exposure is
(a) 3 s
(b) 12 s
(c) 24 s
(d) 48 sdigAnsr: CAns : Correct option
(b)
Here,
`` {d}_{1}=5cm=0.05\,\mathrm{\,m\,}``
`` {d}_{2}=10cm=0.1\,\mathrm{\,m\,}``
`` {t}_{1}=3s``
`` {t}_{2}=?``
`` \,\mathrm{\,Suppose\,}the\,\mathrm{\,actual\,}\,\mathrm{\,incident\,}\,\mathrm{\,illuminance\,}be{E}_{o}``
`` \,\mathrm{\,Suppose\,}the\,\mathrm{\,iluminance\,}at3\,\mathrm{\,cm\,}\,\mathrm{\,distance\,}be{E}_{d1}``
`` \,\mathrm{\,Suppose\,}the\,\mathrm{\,iluminance\,}at10\,\mathrm{\,cm\,}\,\mathrm{\,distance\,}be{E}_{d2}``
`` \,\mathrm{\,cos\,}\theta =1``
`` {E}_{d1}=\frac{{E}_{o}}{{{d}_{1}}^{2}}``
`` \,\mathrm{\,Now\,},``
`` {\,\mathrm{\,t\,}}_{1}\,\mathrm{\,\alpha \,}\frac{1}{{\,\mathrm{\,E\,}}_{\,\mathrm{\,d\,}1}}``
`` \Rightarrow {\,\mathrm{\,t\,}}_{1}=\frac{\,\mathrm{\,k\,}}{{\,\mathrm{\,E\,}}_{\,\mathrm{\,d\,}1}}``
`` \Rightarrow {\,\mathrm{\,t\,}}_{1}=\frac{\,\mathrm{\,k\,}{5}^{2}}{{\,\mathrm{\,E\,}}_{\,\mathrm{\,o\,}}}``
`` \Rightarrow \frac{\,\mathrm{\,k\,}}{{\,\mathrm{\,E\,}}_{\,\mathrm{\,o\,}}}=\frac{3}{25}``
`` S\,\mathrm{\,imilarly\,},``
`` \Rightarrow {\,\mathrm{\,t\,}}_{2}=\frac{\,\mathrm{\,k\,}{10}^{2}}{{\,\mathrm{\,E\,}}_{\,\mathrm{\,o\,}}}``
`` \Rightarrow {\,\mathrm{\,t\,}}_{2}=\frac{3}{25}\times {10}^{2}=12\,\mathrm{\,s\,}``
`` ``
`` ``
`` ``
Page No 454:
- Qstn #9A photographic plate is placed directly in front of a small diffused source in the shape of a circular disc. It takes 12 s to get a good exposure. If the source is rotated by 60° about one of its diameter, the time needed to get the same exposure will be
(a) 6 s
(b) 12 s
(c) 24 s
(d) 48 sdigAnsr: CAns : Correct option
(c)
`` \,\mathrm{\,Here\,},``
`` {t}_{1}=12\,\mathrm{\,s\,}``
`` {\,\mathrm{\,\theta \,}}_{1}={0}^{0}``
`` {\,\mathrm{\,\theta \,}}_{2}={60}^{0}``
`` {\,\mathrm{\,t\,}}_{2}=?``
`` L\,\mathrm{\,et\,}the\,\mathrm{\,distance\,}ber.``
`` L\,\mathrm{\,et\,}the\,\mathrm{\,incident\,}\,\mathrm{\,luminosity\,}be{E}_{o}.``
`` \,\mathrm{\,We\,}\,\mathrm{\,have\,},``
`` {E}_{\theta 1}=\frac{{E}_{o}{\,\mathrm{\,cos\theta \,}}_{1}}{{r}^{2}}``
`` {t}_{1}\alpha \frac{1}{{E}_{\theta 1}}``
`` \Rightarrow {t}_{1}=\frac{{r}^{2}k}{{E}_{o}{\,\mathrm{\,cos\theta \,}}_{1}}``
`` \Rightarrow 12=\frac{{r}^{2}k}{{E}_{o}\,\mathrm{\,cos\,}0}``
`` \Rightarrow \frac{{r}^{2}k}{{E}_{o}}=12``
`` ``
`` S\,\mathrm{\,imilarly\,},``
`` {\,\mathrm{\,t\,}}_{2}=\frac{{\,\mathrm{\,r\,}}^{2}\,\mathrm{\,k\,}}{{\,\mathrm{\,E\,}}_{\,\mathrm{\,o\,}}{\,\mathrm{\,cos\theta \,}}_{2}}=\frac{12}{\,\mathrm{\,cos\,}\left({60}^{0}\right)}``
`` \Rightarrow {\,\mathrm{\,t\,}}_{2}=12\times 2=24\,\mathrm{\,s\,}``
`` ``
Page No 454:
- Qstn #10A point source of light moves in a straight line parallel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distance r from the source as
(a) I ∝ ``\frac{1}{r}``
(b) I ∝ ``\frac{1}{r^2}``
(c)I ∝ ``\frac{1}{r^3}``
(d) I ∝ ``\frac{1}{r^4}``digAnsr: CAns : Correct option
(c)
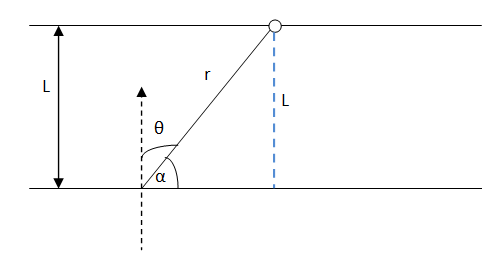
Let the distance between the parallel straight lines be L.
Angle with normal = θ
`` \,\mathrm{\,We\,}\,\mathrm{\,know\,},``
`` I=\frac{{I}_{o}\,\mathrm{\,cos\,}\theta }{{r}^{2}}``
`` \,\mathrm{\,From\,}theabove\,\mathrm{\,fig\,}ure,weget``
`` \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,cos\,}\left({90}^{0}-\,\mathrm{\,\alpha \,}\right)}{{\,\mathrm{\,r\,}}^{2}}``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,sin\alpha \,}}{{\,\mathrm{\,r\,}}^{2}}``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}}{{\,\mathrm{\,r\,}}^{2}}\left(\frac{\,\mathrm{\,L\,}}{\,\mathrm{\,r\,}}\right)``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,L\,}}{{\,\mathrm{\,r\,}}^{3}}``
`` \,\mathrm{\,L\,}=\,\mathrm{\,constant\,}\,\mathrm{\,for\,}\,\mathrm{\,parallel\,}\,\mathrm{\,moving\,}\,\mathrm{\,source\,}``
`` So,{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,L\,}=\,\mathrm{\,k\,}\left(\,\mathrm{\,constant\,}\right)``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{\,\mathrm{\,k\,}}{{\,\mathrm{\,r\,}}^{3}}``
`` \Rightarrow \,\mathrm{\,I \alpha \,}\frac{1}{{\,\mathrm{\,r\,}}^{3}}``
Page No 454:
- Qstn #11Figure shows a glowing mercury tube. The intensities at point A, B and C are related as
(a) B > C > A
(b) A > C > B
(c) B = C > A
(d) B = C < A
FiguredigAnsr: CAns : Correct option
(d)
Here, since B and C have the same distance and lie inclined to make the the same vertical angle with the source, they will have same intensity. But, as A is nearer and forms an angle of 00 with the source, intensity of A will be greater than C or B.
Page No 454:
- #Section : iii
- Qstn #1The brightness-producing capacity of a source
(a) does not depend on its power
(b) does not depend on the wavelength emitted
(c) depends on its power
(d) depends on the wavelength emitted.digAnsr: c,dAns : Correct option
(c) and
(d)
Brightness depends upon how our eyes perceive light. Our eyes perceive yellow colour the most, so brightness depends upon the colour of the source. Now, colour is related to the wavelength of the source; so, brightness depends upon the wavelength as well.
Our eyes detect brightness by the amount of photons actually reaching our retinas. Again, the number of photons depends upon the power of the source. So, brightness depends upon the power of the source too.
Page No 454:
- Qstn #2A room is illuminated by an extended source. The illuminance at a particular portion of a wall can be increased by
(a) moving the source
(b) rotating the source
(c) bringing some mirrors in proper positions
(d) changing the colour of the source.digAnsr: a,b,c,dAns : Correct option
(a),
(b),
(c),
(d) i.e. all the options are correct.
a) Moving the source to the middle will illuminate the surface properly because illuminance depends upon the distance from the source.
b) Rotating the source will also have an effect because illuminance depends upon the angle made by the normal on the surface.
c) Bringing mirrors to the proper position will increase illuminance at that particular portion of the wall by gathering light and focussing them at one point.
d) Our eyes sense some colours as bright and some colours as dull, selecting the colours near yellow will make the wall appear brighter.
Page No 454:
- Qstn #3Mark the correct options.
(a) The luminous efficiency of a monochromatic source is always greater than that of a white light source of same power.
(b) The luminous efficiency of a monochromatic source of wavelength 555 nm is always greater than that of a white light source of same power.
(c) The illuminating power of a monochromatic source of wavelength 555 nm is always greater than that of a white light source of same power.
(d) The illuminating power of a monochromatic source is always greater than that of a white light source of same power.digAnsr: b,cAns : Correct options:
(b) and
(c)
a) The luminous efficiency of a monochromatic source may be less than that of the white light if the former emits wavelength far away from 555 nm.
b) Yes, it is true that our eyes mostly respond to colours close to the wavelength of 555 nm and detect them bright. So, luminous efficiency is unity (highest).
c) It is true because white light distributes its energy amongst certain colours that our eyes cannot detect as brightly as they detect a 555 nm light.
d) It is not necessarily true. If the monochromatic light radiates in a wavelength that is far away from 555 nm, our eyes will not perceive it as bright. So, it will have lesser illuminating power.
Page No 454:
- Qstn #4Mark out the correct options.
(a) Luminous flux and radiant flux have same dimensions.
(b) Luminous flux and luminous intensity have same dimensions.
(c) Radiant flux and power have same dimensions.
(d) Relative luminosity is a dimensionless quantity.digAnsr: b,c,dAns : Correct option
(b),
(c),
(d)
a) No, luminous flux has the dimension of luminous intensity (cd/sr). The dimension of radiant flux is watt.
b) Yes, both have the dimension of luminous intensity, i.e. cd/sr.
c) Yes, both have the dimensions of power.
d) Yes, it is a ratio of same kind of quantities. So, it is dimensionless.
Page No 455:
- #Section : iv
- Qstn #1A source emits 45 joules of energy in 15 s. What is the radiant flux of the source?Ans : Given,
Total energy emitted (E) = 45 J
Time (t) = 15 s
Radiant flux of the source is given by,
`` \,\mathrm{\,Radiant\,}\,\mathrm{\,Flux\,}=\frac{\,\mathrm{\,Total\,}\,\mathrm{\,energy\,}\,\mathrm{\,emitted\,}}{\,\mathrm{\,Time\,}}``
`` =\frac{45}{15}=3\,\mathrm{\,W\,}``
So, the radiant flux of the source is 3 W.
Page No 455:
- Qstn #2A photographic plate records sufficiently intense lines when it is exposed for 12 s to a source of 10 W. How long should it be exposed to a 12 W source radiating the light of same colour to get equally intense lines?Ans : Let t be the time for which the photograph is exposed.
To record the sufficiently intense lines, energy should be same.
Energy = radiant flux × time
= 10 W×12 s
= 12 W×t
`` \Rightarrow t=\frac{10\,\mathrm{\,W\,}\times 12\,\mathrm{\,s\,}}{12\,\mathrm{\,W\,}}``
`` =10\,\mathrm{\,s\,}``
Therefore, the photographic plate should be exposed for 10 s to get equally intense lines.
Page No 455:
- Qstn #3Using figure (22.1), find the relative luminosity of wavelengthAns : From the graph, we can find the following: