20: Dispersion And Spectra : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

20: dispersion and Spectra

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #8
Three thin prisms are combined as shown in figure. The refractive indices of the crown glass for red, yellow and violet rays are μ_r, μ_y and μ_v respectively and those for the flint glass are μ’_r, μ’_y and μ’_v respectively. Find the ratio A‘/A for which
Ans : For the crown glass, we have:
Refractive index for red rays = μ_r
Refractive index for yellow rays = μ_y
Refractive index for violet rays =μ_v
For the flint glass, we have:
Refractive index for red rays = μ'_r
Refractive index for yellow rays = μ'_y
Refractive index for violet rays =μ'_v
Let δ_cyand δ_fybe the angles of deviation produced by the crown and flint prisms for the yellow light.
Total deviation produced by the prism combination for yellow rays:
δ_y = δ_cy - δ_fy
= 2δ_cy - δ_fy
=2(μ_cy + 1)A - (μ_fy - 1)A'
Angular dispersion produced by the combination is given by
δ_v - δ_r = [(μ_vc - 1)A - (μ_vf - 1)A' + (μ_v_c - 1)A - `` \left[\left({\mu }_{rc}-1\right)A-\left({\mu }_{rf}-1\right)A\text{'}+\left({\mu }_{rc}-1\right)A\right]``
Here,
μ_vc₌Refractive index for the violet colour of the crown glass
μ_vf = Refractive index for the violet colour of the flint glass
`` {\mu }_{rc}`` = Refractive index for the red colour of the crown glass
`` {\mu }_{rf}`` = Refractive index for the red colour of the flint glass
On solving, we get:
δ_v - δ_r = 2(μ_vc -1)A - (μ_vf - 1)A'

#8-a
there is no net angular dispersion, and
Ans : For zero angular dispersion, we have:
δ_t - δ_t = 0 = 2(μ_vc -1)A - (μ_vf - 1)A'
`` \Rightarrow \frac{A\text{'}}{A}=\frac{2({\mu }_{\,\mathrm{\,vf\,}}-1)}{({\mu }_{vc}-1)}``
`` =\frac{2({\mu }_{r}-{\mu }_{r})}{({\mu }_{r}-\mu )}``

#8-b
there is no net deviation in the yellow ray.
Figure
Ans : For zero deviation in the yellow ray, δ_y = 0.
⇒ 2(μ_cy - 1)A = (μ_fy - 1)A
`` \Rightarrow \frac{A\text{'}}{A}=\frac{2({\mu }_{\,\mathrm{\,cy\,}}-1)}{({\mu }_{\,\mathrm{\,fy\,}}-1)}``
`` =\frac{2({\mu }_{y}-1)}{(\mu {\text{'}}_{y}-1)}``
Page No 442:
Page No 443:

Qstn #9
A thin prism of crown glass (μ_r = 1.515, μ_v = 1.525) and a thin prism of flint glass (μ_r = 1.612, μ_v = 1.632) are placed in contact with each other. Their refracting angles are 5.0° each and are similarly directed. Calculate the angular dispersion produced by the combination.
Ans :
For crown glass, we have:
Refractive index for red colour, μ_cr = 1.515
Refractive index for violet colour, μ_cv = 1.525
For flint glass, we have:
Refractive index for red colour, μ_fr = 1.612
Refractive index for violet colour,μ_fv = 1.632
Refracting angle, A = 5°
Let:
δ_c = Angle of deviation for crown glass
δ_f= Angle of deviation for flint glass
As prisms are similarly directed and placed in contact with each other, the total deviation produced `` \left(\delta \right)`` is given by
δ = δ_c + δ_f
= (`` {\mu }_{c}`` - 1)A + (`` {\mu }_{f}`` - 1)A
= (`` {\mu }_{c}`` + `` {\mu }_{f}``- 2)A
For violet light, δ_v = (μ_cv + μ_fv - 2)A
For red light, δ_r= (μ_cr + μ_fr - 2)A
Now, we have:
Angular dispersion of the combination:
δ_v - δ_r= (μ_cv + μ_fv - 2)A - (μ_cr + μ_fr - 2)A
= (μ_cv + μ_fv - μ_cr - μ_fr) A
= (1.525 + 1.632 - 1.515 - 1.612)5
= 0.15°
So, the angular dispersion produced by the combination is 0.15°.
Page No 443:

Qstn #10
A thin prism of angle 6.0°, ω = 0.07 and μ_y = 1.50 is combined with another thin prism having ω = 0.08 and μ_y = 1.60. The combination produces no deviation in the mean ray.
Ans : Given:
For the first prism,
Angle of prism, A' = 6°
Angle of deviation, ω' = 0.07
Refractive index for yellow colour, μ'_y = 1.50
For the second prism,
Angle of deviation, ω = 0.08
Refractive index for yellow colour, μ_y= 1.60
Let the angle of prism for the second prism be A.
The prism must be oppositely directed, as the combination produces no deviation in the mean ray.

#10-a
Find the angle of the second prism.
Ans : The deviation of the mean ray is zero.
Thus, we have:
δ_y = (μ_y - 1)A - (μ'_y - 1)A' = 0
`` \therefore `` (1.60 - 1)A = (1.50 - 1)A'
⇒ A = `` \frac{0.50\times 6°}{0.60}=5°``

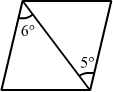
#10-b
Find the net angular dispersion produced by the combination when a beam of white light passes through it.
Ans : Net angular dispersion on passing a beam of white light:
(μ_y - 1)ωA - (μ_y - 1)ω'A'
⇒ (1.60 - 1)(0.08)(5°) - (1.50 - 1)(0.07)(6°)
⇒ 0.24° - 0.21° = 0.03°

#10-c
If the prisms are similarly directed, what will be the deviation in the mean ray?
Ans : For the prisms directed similarly, the net deviation in the mean ray is given by
δ_y = (μ_y - 1)A + (μ_y - 1)A'
= (1.60 - 1)5° + (1.50 - 1)6°
= 3° + 3° = 6°

#10-d
Find the angular dispersion in the situation described in
(c).
Ans : For the prisms directed similarly, angular dispersion is given by
δ_v - δ_r = (μ_y - 1)ωA - (μ_y - 1)ω'A'
= 0.24° + 0.21°
= 0.45°
Page No 443:

Qstn #11
The refractive index of a material M1 changes by 0.014 and that of another material M2 changes by 0.024 as the colour of the light is changed from red to violet. Two thin prisms, one made of M1(A = 5.3°) and the other made of M2(A = 3.7°) are combined with their refracting angles oppositely directed.
Ans : If μ'_v and μ'_rare the refractive indices of material M₁, then we have:
μ'_v - μ'_r = 0.014
If μ_vand μ_r are the refractive indices of material M₂, then we have:
μ_v - μ_r = 0.024
Now,
Angle of prism for M₁_,A' = 5.3°
Angle of prism for M₂, A = 3.7°

#11-a
Find the angular dispersion produced by the combination.
Ans : When the prisms are oppositely directed, angular dispersion `` \left({\delta }_{1}\right)`` is given by
δ₁ = (μ_v - μ_r)A - (μ'_v - μ'_r)A'
On substituting the values, we get:
δ₁ = 0.024 × 3.7° - 0.014 × 5.3°
= 0.0146°
So, the angular dispersion is 0.0146°.

#11-b
The prisms are now combined with their refracting angles similarly directed. Find the angular dispersion produced by the combination.
Ans : When the prisms are similarly directed, angular dispersion`` \left({\delta }_{2}\right)`` is given by
δ₂ = (μ_v - μ_r)A + (μ'_v - μ'_r)A'
On substituting the values, we get:
δ₂ = 0.024 × 3.7° + 0.014 × 5.3°
= 0.163°
So, the angular dispersion is 0.163°.