NEET-XII-Physics
14: Some Mechanical Properties of Matter
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #14If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain.Ans : A mosquito thrown into water has its wings wetted. Now, wet wing surfaces tend to stick together because of the surface tension of water. This does not let the mosquito fly.
Page No 297:
- Qstn #15The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?Ans : The forces act tangentially to the bubble surface on both sides of a given line but they have one component normal to the bubble surface. This component balances the force due to excess pressure inside the bubble.
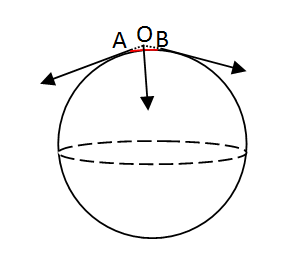
In the figure, let us consider a small length AB on the surface of the spherical bubble. Let the surface forces act tangentially along A and B. On producing the forces backwards, they meet at a point O. By the parallelogram law of forces, we see that the resultant force acts opposite to the normal. This balances the internal forces due to excess pressure.
Page No 297:
- Qstn #16When the size of a soap bubble is increased by pushing more air in it, the surface area increases. Does it mean that the average separation between the surface molecules is increased?Ans : No. The average intermolecular distances do not increase with an increase in the surface area.
A soap bubble's layer consists of several thousand layers of molecules. An increase in the surface area causes the surface energy to also increase. This in turn allows more and more molecules from the inner liquid layers of the bubble to attain potential energy, enabling them to enter the outer surface of the bubble. Hence, the surface area increases.
Page No 298:
- Qstn #17Frictional force between solids operates even when they do not move with respect to each other. Do we have viscous force acting between two layers even if there is no relative motion?Ans : No. For a liquid at rest, no viscous forces exist.
Viscous forces oppose relative motion between the layers of a liquid. These layers do not exist in a liquid that is at rest. Therefore, it is obvious that viscous forces are non-existent in a static liquid.
Page No 298:
- Qstn #18Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.Ans : The motion of any liquid is dependent upon the amount of stress acting on it. The motion of one layer of liquid is resisted by the other due to the property of viscosity. A river bed remains in a static state. Therefore, any immediate layer of liquid in contact with the river bed will also remain static due to the frictional force. However, the next layer of liquid above this static layer will have a greater velocity due to lesser resistance offered by the static layer. Moving upwards, subsequent layers provide lesser and lesser resistance to the movement of the layers above it. Finally, the topmost layer acquires the maximum velocity. Therefore, for a river, the surface waters flow the fastest.
Page No 298:
- Qstn #19If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?Ans : Castor oil will come to rest more quickly because it has a greater coefficient of viscosity than water.
Castor oil has a higher viscosity than water. It will therefore, lose kinetic energy and come to rest faster than water.
Page No 298:
- #Section : ii
- Qstn #1A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that may be given to a similar rope of diameter 2 cm is
(a) 500 N
(b) 250 N
(c) 1000 N
(d) 2000 NdigAnsr: dAns : (d) 2000 N
`` {\,\mathrm{\,F\,}}_{1}=500\,\mathrm{\,N\,}``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,the\,}\,\mathrm{\,required\,}\,\mathrm{\,breaking\,}\,\mathrm{\,force\,}\,\mathrm{\,on\,}\,\mathrm{\,the\,}2\,\mathrm{\,cm\,}\,\mathrm{\,wire\,}\,\mathrm{\,be\,}\,\mathrm{\,F\,}.``
`` \,\mathrm{\,Breaking\,}\,\mathrm{\,stress\,}\,\mathrm{\,in\,}1\,\mathrm{\,cm\,}\,\mathrm{\,wire\,}=\frac{{\,\mathrm{\,F\,}}_{1}}{{\,\mathrm{\,A\,}}_{1}}=\frac{500}{\,\mathrm{\,\pi \,}{\left({\displaystyle \frac{0.01}{2}}\right)}^{2}}``
`` \,\mathrm{\,Breaking\,}\,\mathrm{\,stress\,}\,\mathrm{\,in\,}2\,\mathrm{\,cm\,}\,\mathrm{\,wire\,}=\frac{{\,\mathrm{\,F\,}}_{2}}{{\,\mathrm{\,A\,}}_{2}}=\frac{{\,\mathrm{\,F\,}}_{2}}{\,\mathrm{\,\pi \,}{\left({\displaystyle \frac{0.02}{2}}\right)}^{2}}``
`` \,\mathrm{\,The\,}\,\mathrm{\,breaking\,}\,\mathrm{\,stress\,}\,\mathrm{\,is\,}\,\mathrm{\,the\,}\,\mathrm{\,same\,}\,\mathrm{\,for\,}\,\mathrm{\,a\,}\,\mathrm{\,material\,}.``
`` \Rightarrow \frac{500}{\,\mathrm{\,\pi \,}{\left({\displaystyle \frac{0.01}{2}}\right)}^{2}}=\frac{{\,\mathrm{\,F\,}}_{2}}{\,\mathrm{\,\pi \,}{\left({\displaystyle \frac{0.02}{2}}\right)}^{2}}``
`` =>{\,\mathrm{\,F\,}}_{2}=2000\,\mathrm{\,N\,}``
Page No 298:
- Qstn #2The breaking stress of a wire depends on
(a) material of the wire
(b) length of the wire
(c) radius of the wire
(d) shape of he cross section.digAnsr: aAns : (a)
Breaking stress depends upon the intermolecular/ inter-atomic forces of attraction within materials. In other words, it depends upon the material of the wire.
Page No 298:
- Qstn #3A wire can sustain the weight of 20 kg before breaking. If the wire is cut into two equal parts, each part can sustain a weight of
(a) 10 kg
(b) 20 kg
(c) 40 kg
(d) 80 kgdigAnsr: bAns : (b) 20 kg
As the wire is cut into two equal parts, both have equal cross-sectional areas. Therefore, a weight of 20 kg exerts a force of 20g on both the pieces. Breaking stress depends upon the material of the wire. Since 20g of force is exerted on wires with equal cross-sectional areas, both the wires can sustain a weight of 20 kg.
Page No 298:
- Qstn #4Two wires A and B are made of same material. The wire A has a length l and diameter r while the wire B has a length 2l and diameter r/2. If the two wires are stretched by the same force, the elongation in A divided by the elongation in B is
(a) 1/8
(b) 1/4
(c) 4
(d) 8digAnsr: aAns : (a) 1/8
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,the\,}\,\mathrm{\,Young\,}\text{'}\,\mathrm{\,s\,}\,\mathrm{\,modulus\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}\text{'}\,\mathrm{\,s\,}\,\mathrm{\,material\,}\,\mathrm{\,be\,}\,\mathrm{\,Y\,}.``
`` \,\mathrm{\,Here\,}:``
`` \,\mathrm{\,Force\,}=\,\mathrm{\,F\,}``
`` {\,\mathrm{\,A\,}}_{1}={\,\mathrm{\,\pi r\,}}^{2}``
`` {\,\mathrm{\,L\,}}_{1}=\,\mathrm{\,l\,}``
`` {\,\mathrm{\,A\,}}_{2}=\,\mathrm{\,\pi \,}{\left(\frac{\,\mathrm{\,r\,}}{2}\right)}^{2}=\frac{{\,\mathrm{\,\pi r\,}}^{2}}{4}``
`` {\,\mathrm{\,L\,}}_{2}=2\,\mathrm{\,l\,}``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,the\,}\,\mathrm{\,elongation\,}\,\mathrm{\,in\,}\,\mathrm{\,A\,}\,\mathrm{\,be\,}\,\mathrm{\,x\,}\,\mathrm{\,and\,}\,\mathrm{\,that\,}\,\mathrm{\,in\,}\,\mathrm{\,B\,}\,\mathrm{\,be\,}\,\mathrm{\,y\,}.``
`` ``
`` \,\mathrm{\,Since\,}\,\mathrm{\,the\,}\,\mathrm{\,Young\,}\text{'}\,\mathrm{\,s\,}\,\mathrm{\,modulus\,}\,\mathrm{\,for\,}\,\mathrm{\,both\,}\,\mathrm{\,the\,}\,\mathrm{\,wires\,}\,\mathrm{\,is\,}\,\mathrm{\,the\,}\,\mathrm{\,same\,}:``
`` \,\mathrm{\,Y\,}=\frac{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,F\,}$}\!\left/ \!\raisebox{-1ex}{${\,\mathrm{\,A\,}}_{1}$}\right.}}{{\displaystyle \raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$l$}\right.}}=\frac{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,F\,}$}\!\left/ \!\raisebox{-1ex}{${\,\mathrm{\,A\,}}_{2}$}\right.}}{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,y\,}$}\!\left/ \!\raisebox{-1ex}{$2\,\mathrm{\,l\,}$}\right.}}``
`` \Rightarrow \frac{\,\mathrm{\,x\,}}{\,\mathrm{\,y\,}}=\frac{{\,\mathrm{\,A\,}}_{2}}{2{\,\mathrm{\,A\,}}_{1}}``
`` \Rightarrow \frac{\,\mathrm{\,x\,}}{\,\mathrm{\,y\,}}=\frac{1}{8}``
Page No 298:
- Qstn #5A wire elongates by 1.0 mm when a load W is hung from it. If this wire goes over a a pulley and two weights W each are hung at the two ends, he elongation of he wire will be
(a) 0.5 m
(b) 1.0 mm
(c) 2.0 mm
(d) 4.0 mmdigAnsr: bAns : (b) 1.0 mm
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,the\,}\,\mathrm{\,Young\,}\text{'}\,\mathrm{\,s\,}\,\mathrm{\,modulus\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,material\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}\,\mathrm{\,be\,}\,\mathrm{\,Y\,}.``
`` \,\mathrm{\,Force\,}=\,\mathrm{\,Weight\,}=\,\mathrm{\,W\,}\left(\,\mathrm{\,given\,}\right)``
`` \,\mathrm{\,Suppose\,}C.S.A.\hspace{0.17em}=\,\mathrm{\,A\,}``
`` \,\mathrm{\,x\,}=1\,\mathrm{\,mm\,}=\,\mathrm{\,Elongation\,}\,\mathrm{\,in\,}\,\mathrm{\,the\,}\,\mathrm{\,first\,}\,\mathrm{\,case\,}``
`` \,\mathrm{\,Length\,}=\,\mathrm{\,L\,}``
`` \,\mathrm{\,Y\,}=\frac{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,W\,}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,x\,}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,L\,}$}\right.}}=\frac{\,\mathrm{\,WL\,}}{\,\mathrm{\,Ax\,}}``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,y\,}\,\mathrm{\,be\,}\,\mathrm{\,the\,}\,\mathrm{\,elongation\,}\,\mathrm{\,on\,}\,\mathrm{\,one\,}\,\mathrm{\,side\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}\,\mathrm{\,when\,}\,\mathrm{\,put\,}\,\mathrm{\,in\,}\,\mathrm{\,a\,}\,\mathrm{\,pulley\,}.``
`` \,\mathrm{\,When\,}\,\mathrm{\,put\,}\,\mathrm{\,in\,}\,\mathrm{\,a\,}\,\mathrm{\,pulley\,},\,\mathrm{\,the\,}\,\mathrm{\,length\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}\,\mathrm{\,on\,}\,\mathrm{\,each\,}\,\mathrm{\,side\,}=\frac{\,\mathrm{\,L\,}}{2}``
`` \frac{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,W\,}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,y\,}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \frac{\,\mathrm{\,L\,}}{2}}$}\right.}}=\,\mathrm{\,Y\,}``
`` \Rightarrow \frac{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,W\,}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\,\mathrm{\,y\,}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \frac{\,\mathrm{\,L\,}}{2}}$}\right.}}=\frac{\,\mathrm{\,WL\,}}{\,\mathrm{\,Ax\,}}``
`` \Rightarrow \,\mathrm{\,y\,}=\frac{\,\mathrm{\,x\,}}{2}``
`` \,\mathrm{\,Total\,}\,\mathrm{\,elongation\,}\,\mathrm{\,in\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}=2\,\mathrm{\,y\,}=2\left(\frac{\,\mathrm{\,x\,}}{2}\right)=\,\mathrm{\,x\,}=1\,\mathrm{\,mm\,}``
`` ``
`` ``
`` ``
`` ``
`` ``
Page No 298:
- Qstn #6A heave uniform rod is hanging vertically form a fixed support. It is stretched by its won weight. The diameter of the rod is
(a) smallest at the top and gradually increases down the rod
(b) largest at the top and gradually decreased down the rod
(c) uniform everywhere
(d) maximum in the middle.digAnsr: aAns : (a) smallest at the top and gradually increases down the rod
As the rod is of uniform mass distribution and stretched by its own weight, the topmost part of the rod experiences maximum stress due to the weight of the entire rod. This stress leads to lateral strain and the rod becomes thinner. Moving down along the length of the rod, the stress decreases because the lower parts bear lesser weight of the rod. With reduced stress, the lateral strain also reduces. Hence, the diameter of the rod gradually increases from top to bottom.
Page No 298:
- Qstn #7When a metal wire is stretched by a load, the fractional change in its volume &traingle;V/V is proportional to
(a)
∆ll
(b)
∆ll2
(c)
∆l/l
(d) none of thesedigAnsr: aAns : (a)
`` C.S.A.\hspace{0.17em}=\,\mathrm{\,A\,}``
`` \,\mathrm{\,Length\,}=\,\mathrm{\,l\,}``
`` \,\mathrm{\,Volume\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}\,\mathrm{\,V\,}=\,\mathrm{\,Al\,}``
`` \,\mathrm{\,Assuming\,}\,\mathrm{\,no\,}\,\mathrm{\,lateral\,}\,\mathrm{\,strain\,}\,\mathrm{\,when\,}\,\mathrm{\,longitudinal\,}\,\mathrm{\,strain\,}\,\mathrm{\,occurs\,}:``
`` \,\mathrm{\,Increase\,}\,\mathrm{\,in\,}\,\mathrm{\,volume\,}:∆\,\mathrm{\,V\,}=\,\mathrm{\,A\,}∆\,\mathrm{\,l\,}``
`` \Rightarrow \frac{∆\,\mathrm{\,V\,}}{\,\mathrm{\,V\,}}=\frac{\,\mathrm{\,A\,}∆\,\mathrm{\,l\,}}{\,\mathrm{\,Al\,}}=\frac{∆\,\mathrm{\,l\,}}{\,\mathrm{\,l\,}}``
`` \,\mathrm{\,So\,},\frac{∆\,\mathrm{\,V\,}}{\,\mathrm{\,V\,}}\,\mathrm{\,is\,}\,\mathrm{\,directly\,}\,\mathrm{\,proportional\,}\,\mathrm{\,to\,}\frac{∆\,\mathrm{\,l\,}}{\,\mathrm{\,l\,}}.``
`` ``
Page No 298:
- Qstn #8The length of a metal wire is l1 when the tension in it T1 and is l2 when the tension is T2. The natural length of the wire is
(a)
l1+l22
(b)
l1l2
(c)
l1T2-l2T1T2-T1
(d)
l1T2+l2T1T2+T1digAnsr: cAns : (c)
)`` \,\mathrm{\,Suppose\,}\,\mathrm{\,the\,}\,\mathrm{\,Young\,}\text{'}\,\mathrm{\,s\,}\,\mathrm{\,modulus\,}\,\mathrm{\,be\,}\,\mathrm{\,Y\,}.``
`` C.S.A.\hspace{0.17em}=\,\mathrm{\,A\,}``
`` \,\mathrm{\,Actual\,}\,\mathrm{\,length\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,}=\,\mathrm{\,L\,}``
`` \,\mathrm{\,For\,}\,\mathrm{\,tension\,}{\,\mathrm{\,T\,}}_{1}:``
`` \,\mathrm{\,Y\,}=\frac{{\displaystyle \raisebox{1ex}{${\,\mathrm{\,T\,}}_{1}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\left(\,\mathrm{\,L\,}-{\,\mathrm{\,l\,}}_{1}\right)$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,L\,}$}\right.}}...\left(1\right)``
`` \,\mathrm{\,For\,}\,\mathrm{\,tension\,}{\,\mathrm{\,T\,}}_{2}:``
`` \,\mathrm{\,Y\,}=\frac{{\displaystyle \raisebox{1ex}{${\,\mathrm{\,T\,}}_{2}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\left(\,\mathrm{\,L\,}-{\,\mathrm{\,l\,}}_{2}\right)$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,L\,}$}\right.}}...\left(2\right)``
`` \,\mathrm{\,From\,}\left(1\right)\,\mathrm{\,and\,}\left(2\right):``
`` ``
`` \frac{{\displaystyle \raisebox{1ex}{${\,\mathrm{\,T\,}}_{1}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\left(\,\mathrm{\,L\,}-{\,\mathrm{\,l\,}}_{1}\right)$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,L\,}$}\right.}}=\frac{{\displaystyle \raisebox{1ex}{${\,\mathrm{\,T\,}}_{2}$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,A\,}$}\right.}}{{\displaystyle \raisebox{1ex}{$\left(\,\mathrm{\,L\,}-{\,\mathrm{\,l\,}}_{2}\right)$}\!\left/ \!\raisebox{-1ex}{$\,\mathrm{\,L\,}$}\right.}}``
`` \Rightarrow \frac{{\,\mathrm{\,T\,}}_{1}}{\left(\,\mathrm{\,L\,}-{\,\mathrm{\,l\,}}_{1}\right)}=\frac{{\,\mathrm{\,T\,}}_{2}}{\left(\,\mathrm{\,L\,}-{\,\mathrm{\,l\,}}_{2}\right)}``
`` \Rightarrow \,\mathrm{\,L\,}=\frac{{\,\mathrm{\,T\,}}_{2}{\,\mathrm{\,l\,}}_{1}-{\,\mathrm{\,T\,}}_{1}{\,\mathrm{\,l\,}}_{2}}{{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}}``
Page No 298: