NEET-XII-Physics
11: Gravitation
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #29The time taken by Mars to revolve round the Sun is 1.88 years. Find the ratio of average distance between Mars and the sun to that between the earth and the sun.Ans : According to Kepler's laws of planetary motion, the time period of revolution of a planet about the Sun is directly proportional to the cube of the distance between their centres.
i.e., T2 `` \propto `` R3
`` \Rightarrow \frac{{T}_{m}^{2}}{{T}_{e}^{2}}=\frac{{R}_{m}^{3}}{{R}_{e}^{3}}``
`` \Rightarrow {\left(\frac{{R}_{\,\mathrm{\,m\,}}}{{R}_{\,\mathrm{\,e\,}}}\right)}^{3}={\left(\frac{1.88}{1}\right)}^{2}``
`` \therefore \frac{{R}_{\,\mathrm{\,m\,}}}{{R}_{\,\mathrm{\,e\,}}}={\left(1.88\right)}^{2/3}=1.52``
Page No 227:
- Qstn #30The moon takes about 27.3 days to revolve round the earth in a nearly circular orbit of radius 3.84 × 105 km/ Calculate the mass of the earth from these data.Ans : Time period of rotation of the Moon around the Earth is given by
`` T=2\,\mathrm{\,\pi \,}\sqrt{\frac{{r}^{3}}{\,\mathrm{\,G\,}M}}``,
where r is the distance between the centres of the Earth and Moon and m is the mass of the Earth.
`` \,\mathrm{\,Now\,},27.3=2\times 3.14\sqrt{\frac{{\left(3.84\times {10}^{5}\right)}^{3}}{6.67\times {10}^{-11}M}}``
`` \Rightarrow 27.3\times 27.3=\frac{2\times 3.14\times {\left(3.84\times {10}^{5}\right)}^{3}}{6.67\times {10}^{-11}M}``
`` \Rightarrow M=\frac{2\times {\left(3.14\right)}^{2}\times {\left(3.84\right)}^{3}\times {10}^{15}}{3.335\times {10}^{-11}\times {\left(27.3\right)}^{2}}``
`` =6.02\times {10}^{24}\,\mathrm{\,kg\,}``
∴ The mass of the Earth is found to be 6.02 × 1024 kg.
Page No 227:
- Qstn #31A Mars satellite moving in an orbit of radius 9.4 × 103 km takes 27540 s to complete one revolution. Calculate the mass of Mars.Ans : Time period of revolution of the satellite around the Mars is give by
`` T=2\,\mathrm{\,\pi \,}\sqrt{\frac{{r}^{3}}{\,\mathrm{\,G\,}M}}``,
where M is the mass of the Mars and r is the distance of the satellite from the centre of the planet.
`` \,\mathrm{\,Now\,},27540=2\times 3.14\sqrt{\frac{{\left(9.4\times {10}^{3}\times {10}^{3}\right)}^{3}}{6.67\times {10}^{-11}\times \,\mathrm{\,M\,}}}``
`` \Rightarrow {\left(27540\right)}^{2}={\left(6.28\right)}^{2}\times \frac{{\left(9.4\times {10}^{5}\right)}^{3}}{6.67\times {10}^{-11}\times \,\mathrm{\,M\,}}``
`` \Rightarrow M=\frac{{\left(6.28\right)}^{2}\times {\left(9.4\right)}^{3}\times {10}^{18}}{6.67\times {10}^{-11}\times {\left(27540\right)}^{2}}``
`` \Rightarrow M=6.5\times {10}^{23}\,\mathrm{\,kg\,}``
Page No 227:
- Qstn #32A satellite of mass 1000 kg is supposed to orbit the earth at a height of 2000 km above the earth’s surface. Find
- #32-aits speed in the orbit,Ans : Speed of the satellite in its orbit
`` v=\sqrt{\frac{\,\mathrm{\,G\,}M}{r+h}}=\sqrt{\frac{g{r}^{2}}{r+h}}``
`` \Rightarrow v=\sqrt{\frac{9.8\times {\left(6400\times {10}^{3}\right)}^{2}}{{10}^{6}\times \left(6.4+2\right)}}``
`` \Rightarrow v=\sqrt{\frac{9.8\times 6.4\times 6.4\times {10}^{6}}{8.4}}``
`` \Rightarrow v=6.9\times {10}^{3}\,\mathrm{\,m\,}/\,\mathrm{\,s\,}=6.9\,\mathrm{\,km\,}/\,\mathrm{\,s\,}``
- #32-bis kinetic energy,Ans : Kinetic energy of the satellite
`` \,\mathrm{\,K\,}.\,\mathrm{\,E\,}.=\frac{1}{2}m{v}^{2}``
`` =\frac{1}{2}\times 1000\times {\left(6.9\times {10}^{3}\right)}^{2}``
`` =\frac{1}{2}\times 1000\times \left(47.6\times {10}^{6}\right)``
`` =2.38\times {10}^{10}\,\mathrm{\,J\,}``
- #32-cthe potential energy of the earth-satellite system andAns : Potential energy of the satellite
`` \,\mathrm{\,P\,}.\,\mathrm{\,E\,}.=-\frac{\,\mathrm{\,GM\,}m}{\left(\,\mathrm{\,R\,}+h\right)}``
`` =-\frac{6.67\times {10}^{-11}\times 6\times {10}^{24}\times {10}^{3}}{\left(6400+2000\right)\times {10}^{3}}``
`` =\frac{40\times {10}^{13}}{8400}=-4.76\times {10}^{10}\,\mathrm{\,J\,}``
- #32-dits time period. Mass of the earth = 6 × 1024 kg.Ans : Time period of the satellite
`` T=\frac{2\,\mathrm{\,\pi \,}\left(r+h\right)}{\,\mathrm{\,v\,}}``
`` =\frac{2\times 3.14\times 8400\times {10}^{3}}{6.9\times {10}^{3}}``
`` =\frac{6.28\times 84\times {10}^{2}}{6.9}``
`` =76.6\times 10.2\,\mathrm{\,s\,}``
`` =2.1\,\mathrm{\,h\,}``
Page No 227:
- #33
- #33-aFind the radius of the circular orbit of a satellite moving with an angular speed equal to the angular speed of earth’s rotation.Ans : The angular speed of the Earth and the satellite will be the same.
`` \,\mathrm{\,i\,}.\,\mathrm{\,e\,}.,\frac{2\,\mathrm{\,\pi \,}}{{T}_{e}}=\frac{2\,\mathrm{\,\pi \,}}{{T}_{s}}``
`` \Rightarrow \frac{1}{24\times 3600}=\frac{1}{2\,\mathrm{\,\pi \,}\sqrt{{\left(R+h\right)}^{3}/g{h}^{2}}}``
`` \Rightarrow 12\times 3600=3.14\sqrt{\frac{{\left(R+h\right)}^{3}}{g{R}^{2}}}``
`` \Rightarrow \frac{{\left(\,\mathrm{\,R\,}+h\right)}^{3}}{g{\,\mathrm{\,R\,}}^{2}}=\frac{{\left(12\times 3600\right)}^{2}}{{\left(3.14\right)}^{2}}``
`` \Rightarrow \frac{\left(6400+{h}^{3}\right)\times {10}^{9}}{9.8\times {\left(6400\right)}^{2}\times {10}^{6}}=\frac{{\left(12\times 3600\right)}^{2}}{{\left(3.14\right)}^{2}}``
`` \Rightarrow \frac{\left(6400+h\right)\times {10}^{9}}{6272\times {10}^{9}}=432\times {10}^{4}``
`` \Rightarrow {\left(6400+h\right)}^{3}=6272\times 432\times {10}^{4}``
`` \Rightarrow 6400+h={\left(6272\times 432\times {10}^{4}\right)}^{1/3}-6400``
`` \Rightarrow h=42300\,\mathrm{\,km\,}``
- #33-bIf the satellite is directly above the North Pole at some instant, find the time it takes to come over the equatorial plane. Mass of the earth = 6 × 1024 kg.Ans : Time taken from the North Pole to the equatorial plane is given by
`` \frac{1}{4}\,\mathrm{\,T\,}``
`` =\frac{1}{4}\times 6.28\sqrt{\frac{{\left(42300+6400\right)}^{3}}{10\times {\left(6400\right)}^{2}\times {10}^{6}}}``
`` =3.14\sqrt{\frac{{\left(479\right)}^{3}\times {10}^{6}}{{\left(64\right)}^{2}\times {10}^{11}}}``
`` =3.14\sqrt{\frac{497\times 497\times 497}{64\times 64\times {10}^{5}}}``
`` =6\,\mathrm{\,h\,}``
Page No 227:
- Qstn #34What is the true weight of an object in a geostationary satellite that weighed exactly 10.0 N at the north pole?Ans : For a geostationary satellite, we have:
R = 6.4 × 103 km
h = 3.6 × 103 km
Given: mg = 10 N
The true weight of the object in the geostationary satellite is given by
`` mg\text{'}=mg-\frac{{R}^{2}}{{\left(R+h\right)}^{2}}``
`` =10-\frac{{\left(6400\times {10}^{3}\right)}^{2}}{\left(6400\times {10}^{3}+3600\times {10}^{3}\right)}``
`` =10-\left[\frac{{\left(64\times {10}^{5}\right)}^{2}}{\left(6.4\times {10}^{6}+36\times {10}^{5}\right)}\right]``
`` =10-\left[\frac{4096\times {10}^{10}}{{\left(42.4\right)}^{2}\times {10}^{12}}\right]``
`` =\frac{4096}{17980}=0.227\,\mathrm{\,N\,}``
Page No 227:
- Qstn #35The radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. Find the acceleration due to the gravitation of the planet at its surface.Ans : The time period of revolution of the satellite around a planet in terms of the radius of the planet and radius of the orbit of the satellite is given by `` T=2\,\mathrm{\,\pi \,}\sqrt{\frac{{R}_{2}^{2}}{g{R}_{1}^{2}}}``, where g is the acceleration due to gravity at the surface of the planet.
`` \,\mathrm{\,Now\,},{T}^{2}=4{\,\mathrm{\,\pi \,}}^{2}\frac{{R}_{2}^{2}}{g{R}_{1}^{2}}``
`` \Rightarrow g=\frac{4{\,\mathrm{\,\pi \,}}^{2}}{{T}^{2}}\frac{{R}_{2}^{2}}{{R}_{1}^{2}}``
∴ Acceleration due to gravity of the planet = `` \frac{4{\,\mathrm{\,\pi \,}}^{2}}{{T}^{2}}\frac{{R}_{2}^{2}}{{R}_{1}^{2}}``
Page No 227:
- Qstn #36Find the minimum colatitude which can directly receive a signal from a geostationary satellite.Ans : Consider that B is the position of the geostationary satellite.
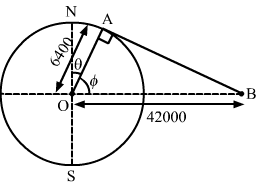
In the given figure, `` \varphi `` is the latitude and θ is the colatitude of a place which can directly receive a signal from a geostationary satellite.
In triangle OAB, we have:
`` \,\mathrm{\,cos\,}\,\mathrm{\,\varphi \,}=\frac{6400}{42000}``
`` =\frac{16}{106}=\frac{8}{53}``
`` \,\mathrm{\,i\,}.\,\mathrm{\,e\,}.,\,\mathrm{\,\varphi \,}={\,\mathrm{\,cos\,}}^{-1}\frac{8}{53}``
`` ={\,\mathrm{\,cos\,}}^{-1}0.15``
`` \,\mathrm{\,Now\,},\theta =\frac{\pi }{2}-\varphi ``
`` \Rightarrow \theta =\frac{\pi }{2}-{\,\mathrm{\,cos\,}}^{-1}0.15``
`` \Rightarrow \theta ={\,\mathrm{\,sin\,}}^{-1}0.15``
Page No 227:
- Qstn #37A particle is fired vertically upward from earth’s surface and it goes up to a maximum height of 6400 km. Find the initial speed of particle.Ans : The particle attained a maximum height 6400 km, which is equal to the radius of the Earth.
Total energy of the particle on the Earth's surface is given by
`` {E}_{e}=\frac{1}{2}M{V}^{2}+\left(\frac{-gmM}{r}\right)....\left(1\right)``
Now, total energy of the particle at the maximum height is given by
`` {E}_{3}=\left(\frac{-GMm}{R\mathit{+}h}\right)+0``
`` \Rightarrow {E}_{3}=\left(\frac{\mathit{-}GMm}{\mathit{2}R}\right)...\left(2\right)\left(\therefore g=R\right)``
From equations (1) and (2), we have:
`` -\frac{GMm}{R}+\frac{1}{2}m{v}^{2}=-\frac{GMm}{2R}``
`` \Rightarrow \left(\frac{1}{2}\right)m{v}^{2}=GMm\left(-\frac{1}{2R}+\frac{1}{R}\right)``
`` \Rightarrow {v}^{2}=\frac{GM}{R}``
`` =\frac{6.67\times {10}^{-11}\times 6\times {10}^{24}}{6400\times {10}^{3}}``
`` =\frac{40.02+{10}^{13}}{6.4\times {10}^{6}}``
`` =6.2\times {10}^{7}=0.62\times {10}^{8}``
`` \therefore v=\sqrt{0.62\times {10}^{8}}``
`` =0.79\times {10}^{4}\,\mathrm{\,m\,}/\,\mathrm{\,s\,}``
`` =79\,\mathrm{\,km\,}/\,\mathrm{\,s\,}``
Page No 227: