NEET-XII-Physics
11: Gravitation
- #9Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.Ans : Consider a small mass element of length dx at a distance x from the centre of the rod.
Mass of the mass element, dm = (M/L) × dx
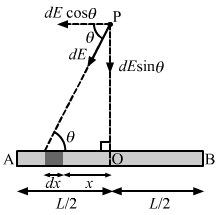
Gravitational field due to this element at point P is given by
`` dE=\frac{\,\mathrm{\,G\,}\left(dm\right)\times 1}{\left({d}^{2}+{x}^{2}\right)}``
The components of the gravitational field due to the symmetrical mass element along the length of the rod cancel each other.
Now, resultant gravitational field = 2dE sin θ
`` =2\times \frac{\,\mathrm{\,G\,}\left(dm\right)}{\left({d}^{2}+{x}^{2}\right)}\times \frac{d}{\sqrt{\left({d}^{2}+{x}^{2}\right)}}``
`` =\frac{2\times GM\times ddx}{L\left({d}^{2}+{x}^{2}\right)\left\{\left(\sqrt{{d}^{2}+{x}^{2}}\right)\right\}}``
Total gravitational field due to the rod at point P is given by
`` E={\int }_{0}^{\,\mathrm{\,L\,}/2}\frac{2Gmddx}{L{\left({d}^{2}+{x}^{2}\right)}^{3/2}}``.
On integrating the above equation, we get:
`` \,\mathrm{\,E\,}=\frac{2\,\mathrm{\,G\,}m}{d\sqrt{{L}^{2}+4{d}^{2}}}``
Page No 226: