NEET-XII-Physics
11: Gravitation
- #8A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.Ans : Consider a small mass element of length dl subtending dθ angle at the centre.
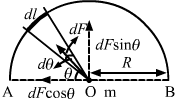
In the semicircle, we can consider a small element dθ.
Then length of the element, dl = R dθ
Mass of the element, dm `` =\left(\frac{\mathit{M}}{\mathit{L}}\right)Rd\,\mathrm{\,\theta \,}``
Force on the mass element is given by
`` d\,\mathrm{\,F\,}=\frac{\,\mathrm{\,G\,}m}{{R}^{2}}dm=\frac{GMRm}{L{R}^{2}}d\theta ``
The symmetric components along AB cancel each other.
Now, net gravitational force on the particle at O is given by
`` F=\int 2dF\,\mathrm{\,sin\,}\,\mathrm{\,\theta \,}``
`` =\int \frac{2GMm}{LR}\,\mathrm{\,sin\,}\,\mathrm{\,\theta \,}d\,\mathrm{\,\theta \,}``
`` \therefore F={\int }_{0}^{\,\mathrm{\,\pi \,}/2}\frac{-2\,\mathrm{\,G\,}Mm}{LR}\,\mathrm{\,sin\,}\,\mathrm{\,\theta \,}d\,\mathrm{\,\theta \,}``
`` =\frac{2\,\mathrm{\,G\,}Mm}{LR}{\left[-\,\mathrm{\,cos\,}\,\mathrm{\,\theta \,}\right]}_{0}^{\,\mathrm{\,\pi \,}/2}``
`` =-2\frac{\,\mathrm{\,G\,}Mm}{LR}\left(-1\right)``
`` =\frac{2\,\mathrm{\,G\,}Mm}{LR}=\frac{2\,\mathrm{\,G\,}Mm}{LL/\,\mathrm{\,\pi \,}}``
`` =\frac{2\,\mathrm{\,\pi G\,}Mm}{{L}^{2}}``
Page No 226: