11: Gravitation : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

11: Gravitation

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #9
Take the effect of bulging of earth and its rotation in account. Consider the following statements:
(A) There are points outside the earth where the value of g is equal to its value at the equator.
(B) There are points outside the earth where the value of g is equal to its value at the poles.
(a) Both A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) Both A and B are wrong.
digAnsr: b
Ans : (b) A is correct but B is wrong.
We know that the value of acceleration due to gravity decreases when we go up from the surface of the Earth. If we take the into account the effect of bulging of the Earth due to its rotation, we can say that acceleration due to gravity is maximum at the poles and minimum at the equator
So, there are points above both the poles where the value of g is equal to its value at the equator.
`` \therefore \,\mathrm{\,F\,}=\frac{4\sqrt{4}\,\mathrm{\,G\,}{m}^{2}}{{a}^{2}}\stackrel{⏜}{\text{j}}``
Page No 225:

Qstn #10
The time period of an earth-satellite in circular orbit is independent of
(a) the mass of the satellite
(b) radius of the orbit
(c) none of them
(d) both of them.
digAnsr: a
Ans : (a) the mass of the satellite
The time period of an earth-satellite in circular orbit is independent of the mass of the satellite, but depends on the radius of the orbit.

Page No 225:

Qstn #11
The magnitude of gravitational potential energy of the moon-earth system is U with zero potential energy at infinite separation. The kinetic energy of the moon with respect to the earth is K.
(a) U < K
(b) U > K
(c) U = K.
digAnsr: b
Ans : (b) U > K
For a system to be bound , total energy of the system should be negative.As we know that kinetic energy can never be negative.
E<0 & K>0 & E=K+U
it gives that U>K.
Page No 225:

Qstn #12
Figure (11-Q2) shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t₁ and t₂ be the time taken by the planet to go from a to b and from c to d respectively,
(a) t₁ < t₂
(b) t₁ = t₂
(c) t₁ > t₂
(d) insufficient information to deduce the relation between t₁ and t₂.
Figure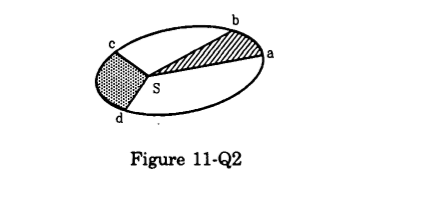
digAnsr: b
Ans : (b) t₁ = t₂
Kepler's second law states that the line joining a planet to the Sun sweeps out equal areas in equal intervals of time, i.e., areal velocity of a planet about the Sun is constant.
The given areas swept by the planet are equal, so t₁ = t₂
Page No 225:

Qstn #13
A person sitting in a chair in a satellite feels weightless because
(a) the earth does not attract the objects in a satellite
(b) the normal force by the chair on the person balances the earth’s attraction
(c) the normal force is zero
(d) the person in satellite is not accelerated.
digAnsr: c
Ans : (c) the normal force is zero
The gravitational pull on the satellite is used up in providing the necessary centripetal force required for its revolution around the earth. This means that there is no net force on the person sitting in a chair in the satellite. So, the normal reaction of the chair on the person is zero and he will feel weightless.
Page No 225:

Qstn #14
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W₁ when the satellite goes in an orbit of radius R and is W₂ when it goes in an orbit of radius 2 -R.
(a) W₁ = W₂
(b) W₁ < W₂
(c) W₁ > W₂
(d)
W1≠W2.
digAnsr: a
Ans : (a) W₁ = W₂
The gravitational pull on the satellite in both cases is used up in providing the necessary centripetal force required for its revolution around the earth. This means that there is no net force acting on the body which has been suspended from a spring balance in the satellite. So, the readings of the spring balance in both the cases are the same and is equal to zero.
Page No 225:

Qstn #15
The kinetic energy needed to project a body of mass m from the earth’ surface to infinity is
(a)
14mgR
(b)
12mgR
(c)
mgR
(d)
2 mgR.
digAnsr: c
Ans : (c) `` mgR``
The kinetic energy needed to project a body of mass m from the Earth's surface to infinity is equal to the negative of the change in potential energy of the body.
i.e., kinetic energy = `` -``(final potential energy `` -`` initial potential energy)
`` \Rightarrow K=-\left(\frac{GMm}{R\text{'}}-\frac{GMm}{R}\right)``
`` \Rightarrow K=-\left(\frac{GMm}{\infty }-\frac{GMm}{R}\right)=\frac{GMm}{R}``
`` \Rightarrow K=mR\times \left(\frac{GM}{{R}^{2}}\right)``
`` \Rightarrow K=mRg\left[\therefore g=\frac{GM}{{R}^{2}}\right]``
Page No 225:

Qstn #16
A particle is kept at rest at a distance R (earth’s radius) above the earth’s surface. The minimum speed with which it should be projected so that it does not return is
(a)
GM4R
(b)
GM2R
(c)
GMR
(d)
2GMR
digAnsr: c
Ans : (c) `` \sqrt{\frac{GM}{R}}``
Potential energy of the particle at a distance R from the surface of the Earth is `` {\left(P.E.\right)}_{i}=\frac{GMm}{(R+R)}=\frac{1}{2}\frac{GMm}{R}``.
Here, M is the mass of the earth; R is the radius of the earth and m is the mass of the body.
Let the particle be projected with speed v so that it just escapes the gravitational pull of the earth.
So, kinetic energy of the body = `` -``[change in the potential energy of the body]
Now, kinetic energy of the body = `` -``[final potential energy `` -`` initial potential energy]
`` \Rightarrow \frac{1}{2}m{v}^{2}=-\left[\frac{GMm}{\infty }-\frac{GMm}{2R}\right]``
`` \Rightarrow v=\sqrt{\frac{GMm}{R}}``
`` ``
Page No 225:

Qstn #17
A satellite is orbiting the earth close to its surface. A particle is to be projected from the satellite to just escape from the earth. The escape speed from the earth is
νe. Its speed with respect to the satellite
(a) will be less than
νe
(b) will be more than
νe
(c) will be equal to
νe
(d) will depend on the direction of projection.
digAnsr: d
Ans : (d) will depend on the direction of projection.For example a body projected vertically requires less escape velocity than a body projected at an angle with the vertical.
Page No 225:

#
Section : iii

Qstn #1
Let V and E denote the gravitational potential and gravitational field at a point. It is possible to have
(a)
V=0 and E=0
(b)
V=0 and E≠0
(c)
V≠0 and E=0
(d)
V≠0 and E≠0.
digAnsr: a,b,c,d
Ans : (a) `` V=0\,\mathrm{\,and\,}E=0``
(b) `` V=0\,\mathrm{\,and\,}E\ne 0``
(c) `` V\ne 0\,\mathrm{\,and\,}E=0``
(d) `` V\ne 0\,\mathrm{\,and\,}E\ne 0``.
All the given conditions for gravitational potential and gravitational field at a point are possible.
Page No 225:

Qstn #2
Inside a uniform spherical shell
(a) the gravitational potential is zero
(b) the gravitational field is zero
(c) the gravitational potential is same everywhere
(d) the gravitational field is same everywhere
digAnsr: b,c,d
Ans : (b) the gravitational field is zero
(c) the gravitational potential is same everywhere
(d) the gravitational field is same everywhere
Inside a uniform spherical shell, the gravitational field is the same everywhere and is equal to zero. The gravitational potential has a constant value inside a uniform spherical shell.
Page No 225:

Qstn #3
A uniform spherical shell gradually shrinks maintaining its shape. The gravitational potential at the centre
(a) increases
(b) decreases
(c) remains constant
(d) oscillates.
digAnsr: b
Ans : (b) decreases
AS it is maintaining its shape so its mass will remain constant which implies that if it shrinks then its volume decreases and to keep the mass constant ,its density increases.Also the gravitational potential at the centre of a uniform spherical shell is inversely proportional to the radius of the shell with a negative sign. When a uniform spherical shell gradually shrinks, the gravitational potential at the centre decreases (because of the negative sign in the formula of potential).
Page No 225:

Qstn #4
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
digAnsr: b,c
Ans : (b) is zero in some parts of the orbit
(c) is zero in one complete revolution
When a planet is moving in an elliptical orbit, at some point, the line joining the centre of the Sun and the planet is perpendicular to the velocity of the planet. For that instant, work done by the gravitational force on the planet becomes zero. As there is no net increase in the speed of the planet after one complete revolution about the Sun, the work done by the gravitational force on the planet in one complete revolution is zero.
Note:For elliptical orbits angle between force ans velocity is always 90 so there the work done is zero in any small part of the orbit.
Page No 225:

Qstn #5
Two satellites A and B move round the earth in the same orbit. The mass of B is twice the mass of A.
(a) Speeds of A and B are equal.
(b) The potential energy of earth+A is same as that of earth+B.
(c) The kinetic energy of A and B are equal.
(d) The total energy of earth+A is same as that of earth+B.
digAnsr: a
Ans : (a) Speeds of A and B are equal.
The orbital speed of a satellite is independent of the mass of the satellite, but it depends on the radius of the orbit. Potential energy, kinetic energy and total energy depend on the mass of the the satellite.
Page No 225: