NEET-XII-Physics
10: Rotational Mechanics
- #17A cubical block of mass M and edge a slides down a rough inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has a magnitude
(a) zero
(b) Mga
(c) Mga sinθ
(d)
12 Mga sinθ.digAnsr: dAns : (d) `` \frac{1}{2}Mga\,\mathrm{\,sin\theta \,}``
Let N be the normal reaction on the block.
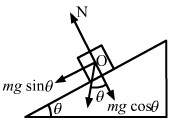
From the free body diagram of the block, it is clear that the forces N and mgcosθ pass through the same line. Therefore, there will be no torque due to N and mgcosθ. The only torque will be produced by mgsinθ.
`` \therefore \stackrel{\to }{\tau }=\stackrel{\to }{F}\times \stackrel{\to }{r}``
`` \,\mathrm{\,Since\,}a\,\mathrm{\,is\,}\,\mathrm{\,the\,}\,\mathrm{\,edge\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,cube\,},r=\frac{a}{2}.``
`` \,\mathrm{\,Thus\,},\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \tau =mg\,\mathrm{\,sin\,}\theta \times \frac{a}{2}``
`` =\frac{1}{2}mga\,\mathrm{\,sin\,}\theta ``
Page No 194: