07: Circular Motion : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

07: Circular Motion

with Solutions - page 7

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#27-c
the tangential acceleration of the block.
Ans : Let a_t be the tangential acceleration of the block.
From figure, we get:
`` -\frac{\mu m{v}^{2}}{R}=m{a}_{t}``
`` \Rightarrow {a}_{t}=-\frac{\mu {v}^{2}}{R}``

#27-d
Integrate the tangential acceleration
dvdt=vdvdsto obtain the speed of the block after one revolution.
Ans : `` \,\mathrm{\,On \,}\,\mathrm{\,using \,}a=\frac{dv}{dt}=v\frac{dv}{ds},\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` v\frac{dv}{ds}=\frac{\mu {v}^{2}}{R}``
`` \Rightarrow ds=-\frac{R}{\mu }\frac{dv}{v}``
`` \,\mathrm{\,Integrating \,}\,\mathrm{\,both \,}\,\mathrm{\,side \,},\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` s=-\frac{R}{\mu }\,\mathrm{\,In \,}v+c``
`` \,\mathrm{\,At \,},s=0,v={v}_{0}``
`` So,c=\frac{R}{\mu }\,\mathrm{\,In \,}{v}_{0}``
`` \Rightarrow s=-\frac{R}{\mu }\,\mathrm{\,In \,}\frac{v}{{v}_{0}}``
`` \Rightarrow \frac{v}{{v}_{0}}={e}^{\mathit{-}\frac{\mu s}{R}}``
`` \mathit{\Rightarrow }v={\,\mathrm{\,v \,}}_{0}{e}^{\mathit{-}\frac{\mathit{\mu s}}{R}}``
`` \,\mathrm{\,For \,}\,\mathrm{\,one \,}\,\mathrm{\,rotation \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` s=2\pi r``
`` \therefore v={v}_{0}{e}^{-2\pi \mu }``
`` ``
`` ``
Page No 116:

Qstn #28
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R. A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
Figure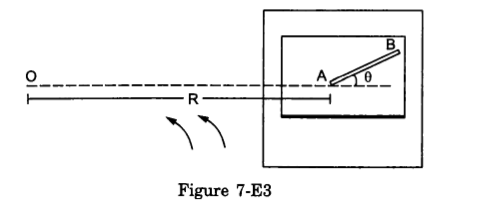
Ans : Let the mass of the particle be m.
Radius of the path = R
Angular velocity = ω
Force experienced by the particle = mω²R
The component of force mRω² along the line AB (making an angle with the radius) provides the necessary force to the particle to move along AB.
`` \therefore m{\omega }^{2}R\,\mathrm{\,cos \,}\theta =ma``
`` \Rightarrow a={\omega }^{2}R\,\mathrm{\,cos \,}\theta ``
`` ``
`` ``
Let the time taken by the particle to reach the point B be t.
`` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\,\mathrm{\,equation \,}\,\mathrm{\,of \,}\,\mathrm{\,motion \,},\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` L=ut\mathit{+}\frac{\mathit{1}}{\mathit{2}}a{t}^{2}``
`` \Rightarrow L=\frac{1}{2}{\omega }^{2}R\,\mathrm{\,cos \,}\theta {t}^{2}``
`` \Rightarrow {t}^{\mathit{2}}=\frac{2L}{{\omega }^{2}R\,\mathrm{\,cos \,}\theta }``
`` \Rightarrow t=\sqrt{\frac{2L}{{\omega }^{2}R\,\mathrm{\,cos \,}\theta }}``
Page No 116:

Qstn #29
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road. A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is . (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
Figure (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
Figure
Ans : Given:
Speed of the car = v = 36 km/h = 10 m/s
Radius of the road = r = 50 m
Friction coefficient between the block and the plate = μ = 0.58
Mass of the small body = m = 100 g = 0.1 kg (a) Let us find the normal contact force (N) exerted by the plant of the block.
`` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}=0.1\times \frac{100}{50}=\frac{1}{5}=0.2`` (b) The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
Therefore, we have:
`` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,cos\theta \,}...\left(\,\mathrm{\,i \,}\right)``
`` \mu \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,sin\theta \,}...\left(ii\right)``
`` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\left(\,\mathrm{\,i \,}\right)\,\mathrm{\,and \,}\left(\,\mathrm{\,ii \,}\right),\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` \frac{\mu m{v}^{2}}{r}\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}\,\mathrm{\,sin \,}\theta ``
`` \Rightarrow \,\mathrm{\,\mu \,}=\,\mathrm{\,tan\theta \,}``
`` \Rightarrow \,\mathrm{\,\theta \,}={\,\mathrm{\,tan \,}}^{-1}(0.58)\approx 30°``
Page No 116: (a) Let us find the normal contact force (N) exerted by the plant of the block.
`` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}=0.1\times \frac{100}{50}=\frac{1}{5}=0.2`` (b) The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
Therefore, we have:
`` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,cos\theta \,}...\left(\,\mathrm{\,i \,}\right)``
`` \mu \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,sin\theta \,}...\left(ii\right)``
`` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\left(\,\mathrm{\,i \,}\right)\,\mathrm{\,and \,}\left(\,\mathrm{\,ii \,}\right),\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` \frac{\mu m{v}^{2}}{r}\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}\,\mathrm{\,sin \,}\theta ``
`` \Rightarrow \,\mathrm{\,\mu \,}=\,\mathrm{\,tan\theta \,}``
`` \Rightarrow \,\mathrm{\,\theta \,}={\,\mathrm{\,tan \,}}^{-1}(0.58)\approx 30°``
Page No 116:

#29-a
Find the normal contact force exerted by the plate on the block.
Ans : Let us find the normal contact force (N) exerted by the plant of the block.
`` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}=0.1\times \frac{100}{50}=\frac{1}{5}=0.2``

#29-b
The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
Figure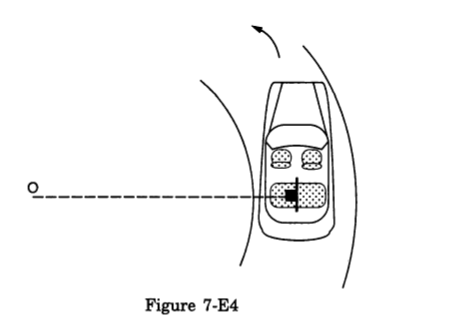
Ans : The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
Therefore, we have:
`` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,cos\theta \,}...\left(\,\mathrm{\,i \,}\right)``
`` \mu \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,sin\theta \,}...\left(ii\right)``
`` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\left(\,\mathrm{\,i \,}\right)\,\mathrm{\,and \,}\left(\,\mathrm{\,ii \,}\right),\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` \frac{\mu m{v}^{2}}{r}\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}\,\mathrm{\,sin \,}\theta ``
`` \Rightarrow \,\mathrm{\,\mu \,}=\,\mathrm{\,tan\theta \,}``
`` \Rightarrow \,\mathrm{\,\theta \,}={\,\mathrm{\,tan \,}}^{-1}(0.58)\approx 30°``
Page No 116:

Qstn #30
A table with smooth horizontal surface is placed in a circle of a large radius R. A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
Figure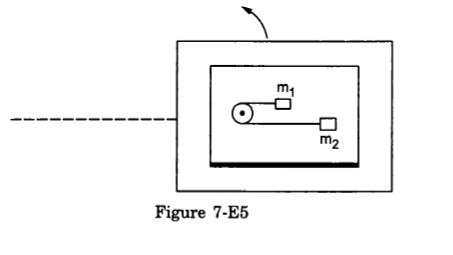
Ans : Let the bigger mass accelerates towards left with acceleration a.
Let T be the tension in the string and ω be the angular velocity of the table.
From the free body diagram, we have:
`` T-ma-m{\omega }^{2}R=0...\left(i\right)``
`` T+2ma-2m{\omega }^{2}R=0...\left(ii\right)``
`` \,\mathrm{\,On \,}\,\mathrm{\,subtracting \,}eq.\left(i\right)\,\mathrm{\,by \,}eq.\left(ii\right),\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` 3ma=m{\omega }^{2}R``
`` \Rightarrow a=\frac{{\omega }^{2}R}{3}``
Substituting the value of a in eq. (i), we get:
`` T=m\left(\frac{{\omega }^{2}R}{3}\right)+m{\omega }^{2}R``
`` \Rightarrow T=\frac{4}{3}m{\omega }^{2}R``