NEET-XII-Physics
07: Circular Motion
- #19-aWhat can its maximum velocity be for which the contact with the road is not broken at the highest point?Ans : At the highest point:
Let m be the mass of the motorcycle and v be the required velocity.
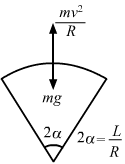
`` mg=\frac{m{v}^{2}}{R}``
`` \Rightarrow {v}^{2}=Rg``
`` \Rightarrow v=\sqrt{Rrg}``
`` ``
`` \left(\,\mathrm{\,b \,}\right)\,\mathrm{\,Given \,}:``
`` v=\left(\frac{1}{\sqrt{2}}\right)\sqrt{Rg}``
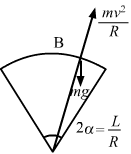
Suppose it loses contact at B.
`` \,\mathrm{\,At \,}\,\mathrm{\,point \,}\,\mathrm{\,B \,},\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` mg\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{R}``
`` \Rightarrow {v}^{2}=Rg\,\mathrm{\,cos \,}\theta ``
`` \,\mathrm{\,Putting \,}\,\mathrm{\,the \,}\,\mathrm{\,value \,}\,\mathrm{\,of \,}v,\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` \sqrt{{\left(\frac{Rg}{2}\right)}^{2}}=Rg\,\mathrm{\,cos \,}\theta ``
`` \Rightarrow \frac{Rg}{2}=Rg\,\mathrm{\,cos \,}\theta ``
`` \Rightarrow \,\mathrm{\,cos \,}\theta =\frac{1}{2}``
`` \Rightarrow \,\mathrm{\,\theta \,}=60°=\frac{\,\mathrm{\,\pi \,}}{3}``
`` \because \theta =\frac{L}{R}``
`` \therefore L=R\theta =\frac{\pi R}{3}``
So, it will lose contact at a distance `` \frac{\pi R}{3}`` from the highest point.
(c) Let the uniform speed on the bridge be v. The chances of losing contact is maximum at the end bridge. We have:

`` \alpha =\frac{L}{2R}``
`` \,\mathrm{\,So \,},\frac{m{v}^{2}}{R}=mg\,\mathrm{\,cos \,}\alpha ``
`` \Rightarrow v=\sqrt{g\,\mathrm{\,Rcos \,}\left(\frac{L}{2R}\right)}``
Page No 115: