Qstnid -Iv-17-a Person Stands On A Spring Balance At The Equator. (A) By What Friction Is The Dinbalance Reag Less Than Hits True Weight? (B) If The Speed Of Earth’s Rotation Is Increased By Such An Amount That The Balance Reading Is Half The True Weight, What Will Be The Length Of The Day In This Case? (A) By What Friction Is The Dinbalance Reag Less Than Hits True Weight? (B) If The Speed Of Earth’s Rotation Is Increased By Such An Amount That The Balance Reading Is Half The True Weight, What Will Be The Length Of The Day In This Case? - 07: Circular Motion

Home Learn Fast select Course

Show Unit/Chapter Change Unit Change Subject Last Menu

NEET-XII-Physics

07: Circular Motion

with Solutions - page 5

Qstn# iv-17 Prvs-Qstn Next-Qstn

#17
A person stands on a spring balance at the equator. (a) By what friction is the dinbalance reag less than hits true weight? (b) If the speed of earth’s rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case? (a) By what friction is the dinbalance reag less than hits true weight? (b) If the speed of earth’s rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
Ans : (a) Balance reading = Normal force on the balance by the Earth.
At equator, the normal force (N) on the spring balance:
N = mg - mω²r
True weight = mg
Therefore, we have:
`` \,\mathrm{\,Fraction \,}\,\mathrm{\,less \,}\,\mathrm{\,than \,}\,\mathrm{\,the \,}\,\mathrm{\,true \,}\,\mathrm{\,weight \,}=\frac{mg-(mg-m{\,\mathrm{\,\omega \,}}^{2}r)}{mg}``
`` =\frac{{\,\mathrm{\,\omega \,}}^{2}r}{g}={\left(\frac{2\,\mathrm{\,\pi \,}}{24\times 3600}\right)}^{2}\left(\frac{6.4\times {10}^{6}}{10}\right)``
`` =3.5\times {10}^{-3}`` (b) When the balance reading is half, we have:
`` \,\mathrm{\,True \,}weight=\frac{mg-m{\,\mathrm{\,\omega \,}}^{2}r}{mg}=\frac{1}{2}``

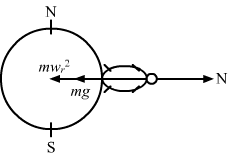
`` \Rightarrow {\,\mathrm{\,\omega \,}}^{2}r=\frac{g}{2}``
`` \Rightarrow \,\mathrm{\,\omega \,}=\sqrt{\frac{g}{2r}}``
`` =\sqrt{\frac{10}{2\times 6400\times {10}^{3}}}\,\mathrm{\,rad \,}/\,\mathrm{\,s \,}``
`` \therefore \,\mathrm{\,Duration \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,day \,}=2\pi \times \sqrt{\frac{2\times 6400\times {10}^{3}}{9.8}}\,\mathrm{\,s \,}``
`` =2\,\mathrm{\,\pi \,}\sqrt{\frac{6.4\times {10}^{7}}{49}}\,\mathrm{\,s \,}``
`` =\frac{2\,\mathrm{\,\pi \,}\times 8000}{7\times 3600}\,\mathrm{\,h \,}=2\,\mathrm{\,h \,}``
Page No 115: (a) Balance reading = Normal force on the balance by the Earth.
At equator, the normal force (N) on the spring balance:
N = mg - mω²r
True weight = mg
Therefore, we have:
`` \,\mathrm{\,Fraction \,}\,\mathrm{\,less \,}\,\mathrm{\,than \,}\,\mathrm{\,the \,}\,\mathrm{\,true \,}\,\mathrm{\,weight \,}=\frac{mg-(mg-m{\,\mathrm{\,\omega \,}}^{2}r)}{mg}``
`` =\frac{{\,\mathrm{\,\omega \,}}^{2}r}{g}={\left(\frac{2\,\mathrm{\,\pi \,}}{24\times 3600}\right)}^{2}\left(\frac{6.4\times {10}^{6}}{10}\right)``
`` =3.5\times {10}^{-3}`` (b) When the balance reading is half, we have:
`` \,\mathrm{\,True \,}weight=\frac{mg-m{\,\mathrm{\,\omega \,}}^{2}r}{mg}=\frac{1}{2}``

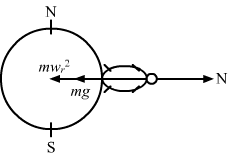
`` \Rightarrow {\,\mathrm{\,\omega \,}}^{2}r=\frac{g}{2}``
`` \Rightarrow \,\mathrm{\,\omega \,}=\sqrt{\frac{g}{2r}}``
`` =\sqrt{\frac{10}{2\times 6400\times {10}^{3}}}\,\mathrm{\,rad \,}/\,\mathrm{\,s \,}``
`` \therefore \,\mathrm{\,Duration \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,day \,}=2\pi \times \sqrt{\frac{2\times 6400\times {10}^{3}}{9.8}}\,\mathrm{\,s \,}``
`` =2\,\mathrm{\,\pi \,}\sqrt{\frac{6.4\times {10}^{7}}{49}}\,\mathrm{\,s \,}``
`` =\frac{2\,\mathrm{\,\pi \,}\times 8000}{7\times 3600}\,\mathrm{\,h \,}=2\,\mathrm{\,h \,}``
Page No 115:

#17-a
By what friction is the dinbalance reag less than hits true weight?
Ans : Balance reading = Normal force on the balance by the Earth.
At equator, the normal force (N) on the spring balance:
N = mg - mω²r
True weight = mg
Therefore, we have:
`` \,\mathrm{\,Fraction \,}\,\mathrm{\,less \,}\,\mathrm{\,than \,}\,\mathrm{\,the \,}\,\mathrm{\,true \,}\,\mathrm{\,weight \,}=\frac{mg-(mg-m{\,\mathrm{\,\omega \,}}^{2}r)}{mg}``
`` =\frac{{\,\mathrm{\,\omega \,}}^{2}r}{g}={\left(\frac{2\,\mathrm{\,\pi \,}}{24\times 3600}\right)}^{2}\left(\frac{6.4\times {10}^{6}}{10}\right)``
`` =3.5\times {10}^{-3}``

#17-b
If the speed of earth’s rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
Ans : When the balance reading is half, we have:
`` \,\mathrm{\,True \,}weight=\frac{mg-m{\,\mathrm{\,\omega \,}}^{2}r}{mg}=\frac{1}{2}``

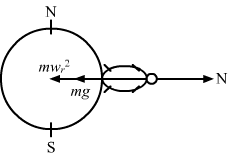
`` \Rightarrow {\,\mathrm{\,\omega \,}}^{2}r=\frac{g}{2}``
`` \Rightarrow \,\mathrm{\,\omega \,}=\sqrt{\frac{g}{2r}}``
`` =\sqrt{\frac{10}{2\times 6400\times {10}^{3}}}\,\mathrm{\,rad \,}/\,\mathrm{\,s \,}``
`` \therefore \,\mathrm{\,Duration \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,day \,}=2\pi \times \sqrt{\frac{2\times 6400\times {10}^{3}}{9.8}}\,\mathrm{\,s \,}``
`` =2\,\mathrm{\,\pi \,}\sqrt{\frac{6.4\times {10}^{7}}{49}}\,\mathrm{\,s \,}``
`` =\frac{2\,\mathrm{\,\pi \,}\times 8000}{7\times 3600}\,\mathrm{\,h \,}=2\,\mathrm{\,h \,}``
Page No 115: