07: Circular Motion : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

07: Circular Motion

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #1
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
digAnsr: a,d
Ans : (a) speed
(d) magnitude of acceleration
When an object follows a curved path, its direction changes continuously. So, the scalar quantities like speed and magnitude of acceleration may remain constant during the motion.
Page No 113:

Qstn #2
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
(a) The average velocity of the earth from 1st jan, 90 to 30th June, 90 is zero.
(b) The average acceleration during the above period is 60 km/s².
(c) The average speed from 1st Jan, 90 to 31st Dec, 90 is zero.
(d) The instantaneous acceleration of the earth points towards the sun.
digAnsr: d
Ans : (d) The instantaneous acceleration of the Earth points towards the Sun.
The speed is constant; therefore, there is no tangential acceleration and the direction of radial acceleration is towards the Sun. So, the instantaneous acceleration of the Earth points towards the Sun.
Page No 113:

Qstn #3
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
digAnsr: b,d
Ans : (b) speed remains constant
(d) tangential acceleration remains constant
If the speed is constant, the position vector of the particle sweeps out equal area in equal time in circular motion.
Also, for constant speed, tangential acceleration is zero, i.e., constant.
Page No 113:

Qstn #4
A particle is going in a spiral path as shown in figure with constant speed.
Figure
(a) The velocity of the particle is constant.
(b) The acceleration of the particle is constant.
(c) The magnitude of acceleration is constant.
(d) The magnitude of acceleration is decreasing continuously.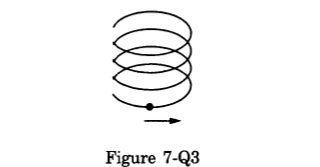
digAnsr: c
Ans : (c) The magnitude of acceleration is constant.
As the pitch and radius of the path is constant, it shows that the magnitude of tangential and radial acceleration is also constant.
Hence, the magnitude of total acceleration is constant.
Page No 114:

Qstn #5
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than
mv2r.
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is
μ=tan-1v2rg.
digAnsr: b,c
Ans : (b) The magnitude of the frictional force on the car is greater than `` \frac{m{v}^{2}}{r}``.
(c) The friction coefficient between the ground and the car is not less than a/g.
If the magnitude of the frictional force on the car is not greater than `` \frac{m{v}^{2}}{r}``, it will not move forward, as its speed (v) is increasing at a rate a.
Page No 114:

Qstn #6
A circular road of radius r is banked for a speed v = 40 km/hr. A car of mass of m attempts to go on the circular road. The friction coefficient between the tyre and the road is negligible.
(a) The are cannot make a turn without skidding.
(b) If the car turns at a speed less than 40 km/hr, it will slip down.
(c) If the car turns at the car is equal to
mv2r.
(d) If the car turns at the correct speed of 40 km/hr, the force by the road on the car is greater than mg as well as greater than
mv2r.
digAnsr: b,d
Ans : (b) If the car turns at a speed less than 40 km/hr, it will slip down.
(d) If the car turns at the correct speed of 40 km/hr, the force by the road on the car is greater than mg as well as greater than `` \frac{m{v}^{2}}{r}``.
The friction is zero and the road is banked for a speed v = 40 km/hr. If the car turns at a speed less than 40 km/hr, it will slip down.
Page No 114:

Qstn #7
A person applies constant force
F→on a particle of mass m and finds that the particle moves in a circle of radius r with a uniform speed v as seen from an inertial frame of reference.
(a) This is not possible.
(b) There are other forces on the particle.
(c) The resultant of the other forces is
mv2rtowards the centre.
(d) The resultant of the other forces varies in magnitude as well as in direction
digAnsr: b,d
Ans : (b) There are other forces on the particle.
(d) The resultant of the other forces varies in magnitude as well as in direction.
We cannot move a particle in a circle by just applying a constant force. So, there are other forces on the particle.
As a constant force cannot move a particle in a circle, the resultant of other forces varies in magnitude as well as in direction (because `` \stackrel{\to }{F}`` is constant).
Page No 114:

#
Section : iv

Qstn #1
Find the acceleration of the moon with respect to the earth from the following data : Distance between the earth and the moon = 3.85 × 10⁵ km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
Ans : Distance between the Earth and the Moon:
`` r=3.85\times {10}^{5}\,\mathrm{\,km \,}=3.85\times {10}^{8}\,\mathrm{\,m \,}``
Time taken by the Moon to revolve around the Earth:
`` T=27.3\,\mathrm{\,days \,}``
`` =24\times 3600\times 27.3\,\mathrm{\,s \,}=2.36\times {10}^{6}\,\mathrm{\,s \,}``
`` ``
`` \,\mathrm{\,Velocity \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,Moon \,}:``
`` v=\frac{2\pi r}{T}``
`` =\frac{2\times 3.14\times 3.85\times {10}^{8}}{2.36\times {10}^{6}}=1025.42\,\mathrm{\,m \,}/\,\mathrm{\,s \,}``
`` \,\mathrm{\,Acceleration \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,Moon \,}:``
`` a=\frac{{v}^{2}}{r}=\frac{(1025.42{)}^{2}}{2.36\times {10}^{6}}=0.00273\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
`` \Rightarrow a=2.73\times {10}^{-3}\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
Page No 114:

Qstn #2
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth’s rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
Ans : Diameter of the Earth = 12800 km
So, radius of the Earth, R = 6400 km = 6.4 × 10⁶ m
Time period of revolution of the Earth about its axis:
`` T=24\,\mathrm{\,hr \,}=24\times 3600\,\mathrm{\,s \,}``
`` v=\frac{2\,\mathrm{\,\pi \,}r}{T}=\frac{2\times 3.14\times 64\times {10}^{6}}{24\times 3600}``^{`` \Rightarrow v=465.185\,\mathrm{\,m \,}/\,\mathrm{\,s \,}``}
`` \,\mathrm{\,Acceleration \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,particle \,}:``
`` \,\mathrm{\,a \,}=\frac{{v}^{\mathit{2}}}{R}=\frac{{\left(465.185\right)}^{2}}{64\times {10}^{5}}=0.038\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
Page No 114:

Qstn #3
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
Ans : Speed is given as a function of time. Therefore, we have:
v = 2t
Radius of the circle = r = 1 cm
At time t = 2 s, we get:

#3-a
Find the radial acceleration of the particle at t = 1 s.
Ans : Radial acceleration
`` a=\frac{{v}^{2}}{r}=\frac{2{}^{2}}{1}=4\,\mathrm{\,cm \,}/{\,\mathrm{\,s \,}}^{2}``

#3-b
Find the tangential acceleration at t = 1 s.
Ans : Tangential acceleration
`` a=\frac{dv}{dt}``
`` =\frac{d}{dt}\left(2t\right)=2\,\mathrm{\,cm \,}/{\,\mathrm{\,s \,}}^{2}``

#3-c
Find the magnitude of the acceleration at t = 1 s.
Ans : Magnitude of acceleration
`` a=\sqrt{{4}^{2}+{2}^{2}}``
`` =\sqrt{20}\,\mathrm{\,cm \,}/{\,\mathrm{\,s \,}}^{2}``
Page No 114:

Qstn #4
A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible?
Ans : Given:
Mass = m = 150 kg
Speed = v = 36 km/hr = 10 m/s
Radius of turn = r = 30 m
Let the horizontal force needed to make the turn be F. We have:
`` F=\frac{m{v}^{2}}{r}=\frac{150\times (10{)}^{2}}{30}``
`` =\frac{150\times 100}{30}=500\,\mathrm{\,N \,}``
Page No 114: