38: Electromagnetic Induction : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

38: Electromagnetic Induction

with Solutions - page 9

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#34-a
Between which pair of points is the emf maximum? What is the value of this maximum emf?
Ans : The maximum value of the emf is between the end points of the diameter perpendicular to the velocity.
The value of the maximum emf is given by
E_max = vB(2R)

#34-b
Between which pair of points is the emf minimum? What is the value of this minimum emf ?
Ans : The minimum value of emf is between the end points of the diameter parallel to the velocity of the ring.
The minimum value of emf is given by
E_min = 0
Page No 308:

Qstn #35
Figure shows a wire sliding on two parallel, conducting rails placed at a separation l. A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity v ?
Figure
Ans : Because the force exerted by the magnetic field on the rod is given by F_magnetic = ilB, the direction of this force is opposite to that of the motion of the rod.
Now, let the external force on it be F.
Because the velocity is constant, the net force acting on the wire must be zero.
Thus, F = F_magnetic = ilB is acting in the direction of the velocity.
Page No 308:

Qstn #36
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
Figure
Ans :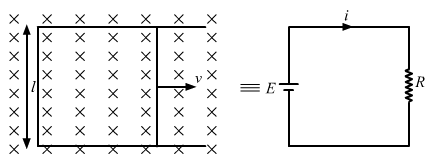
The induced emf is given by
e = Bvl
Total resistance, R = r × Total length of the wire
Because the length of the movable wire is l and the distance travelled by the movable wire in time t is vt, the total length of the loop is 2 (l + vt).
∴ e = i × 2r (l + vt)
Bvl = 2ri (l + vt)
`` \Rightarrow i=\frac{Bvl}{2r(l+vt)}``
Page No 308:

Qstn #37
Consider the situation of the previous problem.
Ans : Emf induced in the circuit, e = Bvl
Current in the circuit, `` i=\frac{e}{R}=\frac{Bvl}{2r(l+vt)}``

#37-a
Calculate the force needed to keep the sliding wire moving with a constant velocity v.
Ans : Force F needed to keep the sliding wire moving with a constant velocity v will be equal in magnitude to the magnetic force on it. The direction of force F will be along the direction of motion of the sliding wire.
Thus, the magnitude of force F is given by
`` F=ilB=\frac{Bvl}{2r(l+vt)}\times lB``
`` =\frac{{B}^{2}{l}^{2}v}{2r(l+vt)}``

#37-b
If the force needed just after t = 0 is F₀, find the time at which the force needed will be F₀/2.
Ans : The magnitude of force F at t = 0 is given by
`` {F}_{0}=ilB=lB\left(\frac{lBv}{2rl}\right)``
`` =\frac{l{B}^{2}v}{2r}...\left(1\right)``
Let at time t = T, the value of the force be F₀/2.
Now,
`` \frac{{F}_{0}}{2}=\frac{{l}^{2}{B}^{2}v}{2r(l+vT)}``
On substituting the value of F₀from (1), we get
`` \frac{l{B}^{2}v}{4r}=\frac{{l}^{2}{B}^{2}v}{2r(l+vT)}``
`` \Rightarrow 2l=l+vT``
`` \Rightarrow T=\frac{l}{v}``
Page No 309:

Qstn #38
Consider the situation shown in figure. The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separated by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangular region and a resistance R connects the rails outside the field region. At t = 0, the wire PQ is pushed towards right with a speed v₀. Find

#38-a
the current in the loop at an instant when the speed of the wire PQ is v,
Ans : When wire PQ is moving with a speed v, the emf induced across it is given by
e = Blv
Total resistance of the circuit = r + R
∴ Current in the circuit, i = `` \frac{Blv}{r+R}``

#38-b
the acceleration of the wire at this instant,
Ans : Force acting on the wire at the given instant, F = ilB
On substituting the value of i from above, we get
`` F=\frac{\left(Blv\right)\left(lB\right)}{(R+r)}=\frac{{B}^{2}{l}^{2}v}{R+r}``
Acceleration of the wire is given by
a`` =\frac{{B}^{2}{l}^{2}v}{m(R+r)}``

#38-c
the velocity v as a functions of x and (d) the maximum distance the wire will move.
Figure
Ans : Velocity can be expressed as:
v = v₀ + at = `` {v}_{0}-\frac{{B}^{2}{l}^{2}v}{m(R+r)}t`` (As force is opposite to velocity)
Velocity as the function of x is given by
`` v={v}_{0}-\frac{{B}^{2}{l}^{2}x}{m(R+r)}``
`` \left(d\right)a=v\frac{dv}{dx}=\frac{{B}^{2}{l}^{2}v}{m(R+r)}``
`` dx=\frac{m(R+r)}{{B}^{2}{l}^{2}}dv``
On integrating both sides, we get
`` x=\frac{m(R+r){v}_{0}}{{B}^{2}{l}^{2}}``
Page No 309:

Qstn #39
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 â„¦. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10^-5 N (figure). It is found that the frame moves with constant speed. Find
Ans : Given:
Total resistance of the frame, R = 2.0 Ω
Magnetic field, B = 0.020 T
Dimensions of the frame:
Length, l = 32 cm = 0.32 m
Breadth, b = 8 cm = 0.08 m

#39-a
this constant speed,
Ans : Let the velocity of the frame be v.
The emf induced in the rectangular frame is given by
e = Blv
Current in the coil, `` i=\frac{Blv}{R}``
The magnetic force on the rectangular frame is given by
F = ilB = 3.2 × 10^-5N
On putting the value of i, we get
`` \frac{{B}^{2}{l}^{2}v}{R}=3.2\times {10}^{-5}``
`` \Rightarrow \frac{(0.020{)}^{2}\times (0.08{)}^{2}\times v}{2}=3.2\times {10}^{-5}``
`` \Rightarrow v=\frac{3.2\times {10}^{-5}}{6.4\times {10}^{-3}\times 4\times {10}^{-4}}``
`` =25\,\mathrm{\,m\,}/\,\mathrm{\,s\,}``

#39-b
the emf induced in the loop,
Ans : Emf induced in the loop, e = vBl
⇒ e = 25 × 0.02 × 0.08
= 4 × 10^-2 V

#39-c
the potential difference between the points a and b and
Ans : Resistance per unit length is given by
r`` =\frac{2}{0.8}``
Ratio of the resistance of part, `` \frac{ad}{cb}=\frac{2\times 0.72}{0.8}=1.8\,\mathrm{\,\Omega \,}``
`` ``
`` {V}_{\,\mathrm{\,ab\,}}=iR=\frac{Blv}{2}\times 1.8``
`` =\frac{0.2\times 0.08\times 25\times 1.8}{2}``
`` =0.036\,\mathrm{\,V\,}=3.6\times {10}^{-2}\,\mathrm{\,V\,}``