38: Electromagnetic Induction : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

38: Electromagnetic Induction

with Solutions - page 10

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#39-d
the potential difference between the points c and d.
Figure
Ans : Resistance of cd:
`` {R}_{\,\mathrm{\,cd\,}}=\frac{2\times 0.8}{0.8}=0.2\,\mathrm{\,\Omega \,}``
`` V=i{R}_{\,\mathrm{\,cd\,}}=\frac{2\times 0.08\times 25\times 0.2}{2}``
`` =4\times {10}^{-3}\,\mathrm{\,V\,}``
Page No 309:

Qstn #40
Figure shows a metallic wire of resistance 0.20 â„¦ sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s^-1. If the horizontal component of the earth’s magnetic field is 3.0 × 10^-5 T, calculate the dip at the place.
Figure
Ans : Given:
Separation between the parallel arms, l = 20 cm = 20 × 10^-2 m
Velocity of the sliding wire, v = 20 cm/s = 20 × 10^-2 m/s
Horizontal component of the earth's magnetic field, B_H = 3 × 10^-5 T
Current through the wire, i = 2 µA = 2 × 10^-6 A
Resistance of the wire, R = 0.2 Ω
Let the vertical component of the earth's magnetic field be B_v and the angle of the dip be δ.
Now,
`` i=\frac{{B}_{v}lv}{R}``
`` ``
`` \Rightarrow {B}_{\,\mathrm{\,v\,}}=\frac{iR}{lv}``
`` =\frac{2\times {10}^{-5}\times 2\times {10}^{-1}}{20\times {10}^{-2}\times 20\times {10}^{-2}}=\frac{2\times 2\times {10}^{-7}}{2\times 2\times {10}^{-2}}``
`` =1\times {10}^{-5}\,\mathrm{\,T\,}``
We know,
`` \,\mathrm{\,tan\,}\delta =\frac{{B}_{\,\mathrm{\,v\,}}}{{B}_{\,\mathrm{\,H\,}}}=\frac{1\times {10}^{-5}}{3\times {10}^{-5}}=\frac{1}{3}``
`` \Rightarrow \delta ={\,\mathrm{\,tan\,}}^{-1}\left(\frac{1}{3}\right)``

Page No 309:

Qstn #41
A wire ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails joined at the bottom as shown in figure. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the region. If the wire slides on the rails at a constant speed v, show that
B=mg R sinθvl2cos2 θFigure
Ans :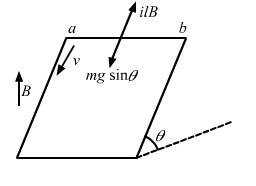
Component of weight along its motion, F' = mgsinθ
The emf induced in the rod due to its motion is given by
e = Bl'v'
Here,
l' = Component of the length of the rod perpendicular to the magnetic field
v' = Component of the velocity of the rod perpendicular to the magnetic field
`` i=\frac{B\times l\times v\,\mathrm{\,cos\theta \,}}{R}``
`` \left|\stackrel{\to }{F}\right|=i\left|\stackrel{\to }{l}\times \stackrel{\to }{B}\right|=ilB\,\mathrm{\,sin\,}(90-\theta )``
`` F=ilB=\frac{Blv\,\mathrm{\,cos\,}\theta }{R}\times l\times B\,\mathrm{\,cos\,}\theta ``
`` F=\frac{{B}^{2}{l}^{2}v{\,\mathrm{\,cos\,}}^{2}\theta }{R}``
`` ``
The direction of force F is opposite to F.'
Because the rod is moving with a constant velocity, the net force on it is zero.
Thus,
F `` -`` F' = 0
F = F'
or
`` \frac{{B}^{2}{l}^{2}v{\,\mathrm{\,cos\,}}^{2}\,\mathrm{\,\theta \,}}{R}=mg\,\mathrm{\,sin\,}\theta ``
`` \therefore B=\sqrt{\frac{Rmg\,\mathrm{\,sin\,}\theta }{{l}^{2}v{\,\mathrm{\,cos\,}}^{2}\theta }}``
Page No 309:

Qstn #42
Consider the situation shown in figure. The wires P₁Q₁ and P₂Q₂ are made to slide on the rails with the same speed 5 cm s^-1. Find the electric current in the 19 â„¦ resistor if

#42-a
both the wires move towards right and
Ans : When both wires move in same direction:
The sliding wires constitute two parallel sources of emf.
The net emf is given by
e = Blv
⇒ e = (1 × 4 × 10^-2) × 5 × (10^-2)
= 20 × 10^-4 V
The resistance of the sliding wires is 2 Ω.
∴ Net resistance = `` \frac{2\times 2}{2+2}`` + 19 = 20 Ω
Net current through 19 Ω = `` \frac{2\times {10}^{-4}}{20}`` = 0.1 mA

#42-b
if P₁Q₁ moves towards left but P₂Q₂ moves towards right.
Figure
Ans : When both wires move in opposite directions with the same speed, the direction of the emf induced in both of them is opposite. Thus, the net emf is zero.
∴ Net current through 19 Ω = 0
Page No 309:

Qstn #43
Suppose the 19 â„¦ resistor of the previous problem is disconnected. Find the current through P₂Q₂ in the two situations

#43-a
and
Ans : When the wires move in the same direction, their polarity remains the same. The circuit remains incomplete. Therefore, no current flows in the circuit.

#43-b
of that problem.
Ans : When the wires move in opposite directions, their polarities are reversed. Thus, current flows in the circuit.
`` {V}_{{\,\mathrm{\,P\,}}_{2}{\,\mathrm{\,Q\,}}_{2}}=Blv``
= 1 × 0.04 × 0.05
= 2 × 10^-3 V
R = 2 Ω
Current in the circuit is given by
`` i=\frac{2\times {10}^{-3}}{2}``
= 1 × 10^-3 A = 1 mA
Page No 309:

Qstn #44
Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s^-1. Find the current in the 10 â„¦ resistor when the switch S is thrown to
Ans : Given:
Magnetic field, B = 1 T
Velocity of the sliding wire, v = 5 × 10^-2 m/s
Resistance of the connected resistor, R = 10 Ω

#44-a
the middle rail
Ans : When the switch is thrown to the middle rail:
Length of the sliding wire = 2 × 10^-2 m
Induced emf, E = Bvl
= 1 × (5 × 10^-2) × (2 × 10^-2) V
= 10 × 10^-4 = 10^-3 V
Current in the 10 Ω resistor is given by
`` i=\frac{E}{R}``
`` =\frac{{10}^{-3}}{10}={10}^{-4}=0.1\,\mathrm{\,mA\,}``

#44-b
the bottom rail.
Figure
Ans : When the switch is thrown to the bottom rail:
The length of the sliding wire becomes 4 × 10^-2 m.
The induced emf is given by
E = Bvl'
= 1 × (5 × 10^-2) × (4 × 10^-2)
= 20 × 10^-4 V
Now,
Current, i = `` \frac{20\times {10}^{-4}}{10}`` A
= 2 × 10^-4 A = 0.2 mA
Page No 309:

Qstn #45
The current generator I_g‘ shown in figure, sends a constant current i through the circuit. The wire cd is fixed and ab is made to slide on the smooth, thick rails with a constant velocity v towards right. Each of these wires has resistance r. Find the current through the wire cd.
Figure
Ans : Current passing through the circuit initially = i
Initial emf = ir
Emf induced due to motion of ab, e = Blv
Net emf, e_net= ir - Blv
Net resistance = 2r
Thus, the current passing through the circuit is `` \frac{ir-Blv}{2r}``.
Page No 309:

Qstn #46
The current generator I_g‘ shown in figure, sends a constant current i through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to I_g. The entire system lies in a vertical magnetic field B. Find the velocity of the wire as a function of time.
Figure
Ans :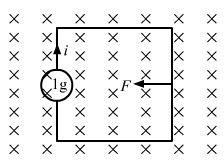
Because current i passes through the sliding wire, the magnetic force on the wire (F) is ilB.
Now,
Acceleration of the sliding wire, a = `` \frac{ilB}{m}``
Velocity of the sliding wire, v = u + at
∵ u = 0
∴ v = `` \frac{ilBt}{m}``
Page No 309:

Qstn #47
The system containing the rails and the wire of the previous problem is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails (figure). It is found that the wire stays in equilibrium. If the wire ab is replaced by another wire of double its mass, how long will it take in falling through a distance equal to its length?
Figure
Ans :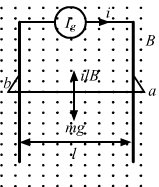
Let us consider the above free body diagram.
As the net force on the wire is zero, ilB = mg.
When the wire is replaced by a wire of double mass, we have

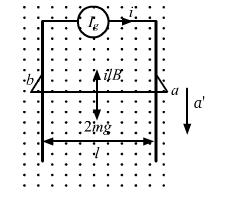
Now, let a' be the acceleration of the wire in downward direction and t be the time taken by the wire to fall.
Net force on the wire = 2mg - ilB = F_net
On applying Newton's second law, we get
2mg - ilB = 2 ma' ...(1)
`` \Rightarrow a\text{'}=\frac{2mg-ilB}{2m}``
`` s=ut+\frac{1}{2}a\text{'}{t}^{2}``
`` \Rightarrow l=\frac{1}{2}\times \frac{2mg-ilB}{2m}\times {t}^{2}[\because s=l]``
`` \Rightarrow t=\sqrt{\frac{4ml}{2mg-ilB}}``
`` \Rightarrow t=\sqrt{\frac{4ml}{2mg-mg}}[\,\mathrm{\,From\,}(1\left)\right]``
`` \Rightarrow t=\sqrt{\frac{2l}{g}}``
Page No 310: