NEET-XII-Physics
38: Electromagnetic Induction
- #41A wire ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails joined at the bottom as shown in figure. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the region. If the wire slides on the rails at a constant speed v, show that
B=mg R sinθvl2cos2 θFigureAns :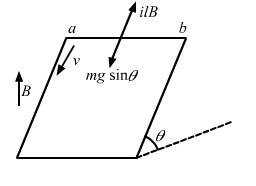
Component of weight along its motion, F' = mgsinθ
The emf induced in the rod due to its motion is given by
e = Bl'v'
Here,
l' = Component of the length of the rod perpendicular to the magnetic field
v' = Component of the velocity of the rod perpendicular to the magnetic field
`` i=\frac{B\times l\times v\,\mathrm{\,cos\theta \,}}{R}``
`` \left|\stackrel{\to }{F}\right|=i\left|\stackrel{\to }{l}\times \stackrel{\to }{B}\right|=ilB\,\mathrm{\,sin\,}(90-\theta )``
`` F=ilB=\frac{Blv\,\mathrm{\,cos\,}\theta }{R}\times l\times B\,\mathrm{\,cos\,}\theta ``
`` F=\frac{{B}^{2}{l}^{2}v{\,\mathrm{\,cos\,}}^{2}\theta }{R}``
`` ``
The direction of force F is opposite to F.'
Because the rod is moving with a constant velocity, the net force on it is zero.
Thus,
F `` -`` F' = 0
F = F'
or
`` \frac{{B}^{2}{l}^{2}v{\,\mathrm{\,cos\,}}^{2}\,\mathrm{\,\theta \,}}{R}=mg\,\mathrm{\,sin\,}\theta ``
`` \therefore B=\sqrt{\frac{Rmg\,\mathrm{\,sin\,}\theta }{{l}^{2}v{\,\mathrm{\,cos\,}}^{2}\theta }}``
Page No 309: