NEET-XII-Physics
36: Permanent Magnets
- #6Show that the magnetic field at a point due to a magnetic dipole is perpendicular to the magnetic axis if the line joining the point with the centre of the dipole makes an angle of
tan-1 2with the magnetic axis.Ans : Given:
Angle made by observation point P with the axis of the dipole, `` \theta `` = `` {\,\mathrm{\,tan\,}}^{-1}\left(\sqrt{2}\right)``
`` \Rightarrow \,\mathrm{\,tan\,}\theta =\sqrt{2}``
`` \Rightarrow 2={\,\mathrm{\,tan\,}}^{2}\theta ``
`` \Rightarrow \,\mathrm{\,tan\,}\theta =\,\mathrm{\,cot\,}\theta ``
`` \Rightarrow \frac{\,\mathrm{\,tan\,}\theta }{2}=\,\mathrm{\,cot\,}\theta ....\left(1\right)``
`` \,\mathrm{\,We\,}\,\mathrm{\,know\,},``
`` \frac{\,\mathrm{\,tan\,}\theta }{2}=\,\mathrm{\,tan\,}\alpha ....\left(2\right)``
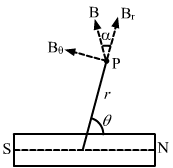
On comparing (1) and (2), we get
tan α = cot θ
`` \Rightarrow ``tan α = tan (90 - θ)
`` \Rightarrow ``α = 90 - θ
`` \Rightarrow ``θ + α = 90°
Hence, the magnetic field due to the dipole is perpendicular to the magnetic axis.
Page No 277: