36: Permanent Magnets : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

36: Permanent Magnets

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #1
Pick the correct options.
(a) Magnetic field is produced by electric charges only
(b) Magnetic poles are only mathematical assumptions having no real existence
(b) A north pole is equivalent to a clockwise current and a south pole is equivalent to an anticlockwise current.
(d) A bar magnet is equivalent to a long, straight current.
digAnsr: a,b,c,d
Ans :
(a) Magnetic field is produced by electric charges only.

(b) Magnetic poles are only mathematical assumptions having no real existence.
Justification of
(a) and
(b):
Investigators and experimenters have failed to find any sign of magnetic monopoles. So, we can assume that magnetic monopoles are only a mathematical assumption.
A magnetic field is produced by the motion of an electric charge only. In paramagnets or ferromagnets, the motion of an electron (charge) and the alignment of domains (bunch of charges with particular alignment) create paramagnetism and ferromagnetism, respectively.
Therefore, the only cause behind the magnetic field is the motion of an electric charge.
Denial of
(c):
The north pole is equivalent to an anticlockwise current and the south pole is equivalent to a clockwise current.
Denial of
(d):
A bar magnet is not equivalent to a long, straight current because the distribution and orientation of magnetic field lines do not resemble each other.
Page No 277:

Qstn #2
A horizontal circular loop carries a current that looks clockwise when viewed from above. It is replaced by an equivalent magnetic dipole consisting of a south pole S and a north pole N.
(a) The line SN should be along a diameter of the loop.
(b) The line SN should be perpendicular to the plane of the loop
(c) The south pole should be slow the loop
(d) The north pole should be below the loop
digAnsr: b,d
Ans : (b) The line SN should be perpendicular to the plane of the loop
(d) The north pole should be below the loop.
A horizontal circular loop carrying current in clockwise direction acts like the south pole of a magnet. Hence, the south pole of the magnet coincides with the loop.

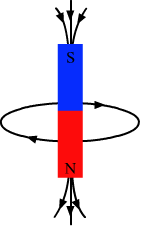
Now, when the loop carrying current in clockwise direction is viewed from above, it looks like the magnetic lines of force are entering the loop thus it acts like south pole of a magnet. And if we view from below the loop then it appears that magnetic lines of force are leaving the loop. Hence, the north pole should be below the loop.
Page No 277:

Qstn #3
Consider a magnetic dipole kept in the north to south direction. Let P₁, P₂, Q₁, Q₂ be four points at the same distance from the dipole towards north, south, east and west of the dipole respectively. The directions of the magnetic field due to the dipole are the same at
(a) P₁ and P₂
(b) Q₁ and Q₂
(c) P₁ and Q₁
(d) P₂ and Q₂
digAnsr: a,b
Ans : (a) P₁ and P₂
(b) Q₁ and Q₂

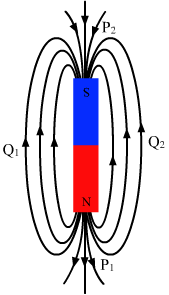
We know that magnetic field lines are directed from the north pole to the south pole. From the given figure, we can say that the direction of magnetic field `` \underset{B}{\to }`` is the same only at points P₁ and P₂ and at points Q₁ and Q₂.
Page No 277:

Qstn #4
Consider the situation of the previous problem. The directions of the magnetic field due to the dipole are opposite at
(a) P₁ and P₂
(b) Q₁ and Q₂
(c) P₁ and Q₁
(d) P₂ and Q₂
digAnsr: c,d
Ans : (c) P₁ and Q₁
(d) P₂ and Q₂

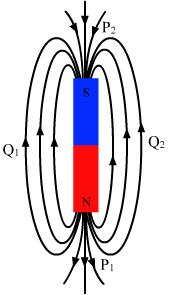
We know that magnetic field lines are directed from the north pole to the south pole. From the given figure, we can say that the direction of the magnetic field `` \underset{B}{\to }`` is opposite at points P₁ and Q₁ and at points P₂ and Q₂.
Page No 277:

Qstn #5
To measure the magnetic moment of a bar magnet, one may use
(a) a tangent galvanometer
(b) a deflection galvanometer if the earth’s horizontal field is known
(c) an oscillation magnetometer if the earth’s horizontal field is known
(d) both deflection and oscillation magnetometer if the earth’s horizontal field is not known
digAnsr: b,c,d,a
Ans : (b) a deflection galvanometer if the earth's horizontal field is known
(c) an oscillation magnetometer if the earth's horizontal field is known
(d) both deflection and oscillation magnetometers if the earth's horizontal field is not known
Denial of
(a):
Tangent galvanometer is an instrument used to measure electric current; it cannot be used to the measure magnetic moment of a bar magnet.
Justification of
(b) and
(c):
Deflection magnetometer is used to measure `` \frac{M}{{B}_{H}}`` of a permanent bar magnet.
Similarly, oscillation magnetometer is used to measure M B_H of a bar magnet. So, if earth's horizontal field, B_H, is known, then the magnetic moment of a bar magnet, M, can be measured.
Justification of
(d):
Using deflection and oscillation magnetometers, we can calculate `` \frac{M}{{B}_{H}}`` and M B_H, respectively. Therefore, if we multiply the result obtained from both the instruments, then B_H cancels out as `` \frac{M}{{B}_{H}}```` \times `` M B_H = M². Thus, the value of B_H is not required.
Therefore, we can use both deflection and oscillation magnetometers if the earth's horizontal field is not known.
Page No 277:

#
Section : iv

Qstn #1
A long bar magnet has a pole strength of 10 Am. Find the magnetic field at a point on the axis of the magnet at a distance of 5 cm from the north pole of the magnet.
Ans : Given:
Pole strength of the bar magnet, m = 10 Am
Distance of the point from the north pole of the bar magnet, r = 5 cm = 0.05 m
We know,
The magnetic field due to magnetic charge `` \left(B\right)`` is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{0}}{4\,\mathrm{\,\pi \,}}\frac{m}{{r}^{\mathit{2}}}``
`` =\frac{{10}^{-7}\times 10}{{\left(5\times {10}^{-2}\right)}^{2}}=\frac{{10}^{-6}}{25\times {10}^{-4}}``
`` =\frac{{10}^{-2}}{25}=4\times {10}^{-4}\,\mathrm{\,T\,}``
Page No 277:

Qstn #2
Two long bare magnets are placed with their axes coinciding in such a way that the north pole of the first magnet is 2.0 cm from the south pole of the second. If both the magnets have a pole strength of 10 Am, find the force exerted by one magnet of the other.
Ans : Given:
Pole strength = m₁= m₂ = 10 Am
Distance between the north pole of the first magnet and the south pole of the second magnet, r = 2 cm = 0.02 m
We know,
Force `` \left(F\right)`` exerted by two magnetic poles on each other is given by
`` F=\frac{{\,\mathrm{\,\mu \,}}_{0}}{4\,\mathrm{\,\pi \,}}\frac{{m}_{1}{m}_{2}}{{r}^{2}}``
`` =\frac{4\,\mathrm{\,\pi \,}\times {10}^{-7}\times {10}^{2}}{4\,\mathrm{\,\pi \,}\times 4\times {10}^{-4}}``
`` =2.5\times {10}^{-2}\,\mathrm{\,N\,}``
Page No 277:

Qstn #3
A uniform magnetic field of 0.20 × 10^-3 T exists in the space. Find the change in the magnetic scalar potential as one moves through 50 cm along the field.
Ans : Given:
Magnetic field in the space, B = 0.20 × 10^-3 T
Distance moved, `` ∆r`` = 50 cm
We know,
`` B=-\frac{dV}{dl}``
`` \Rightarrow dV\mathit{=}{\mathit{\int }}_{{r}_{1}}^{{r}_{2}}\mathit{-}\stackrel{\mathit{\rightharpoonup }}{B\mathit{.}}\,\mathrm{\,d\,}l``
`` ``
Since the magnetic field is uniform, it can come out of the integration sign.
`` \Rightarrow ∆V\mathit{=}\mathit{-}B\mathit{.}(∆r)``
`` ``
Here, `` ∆V`` is the change in the potential.
∴ Change in the potential = -0.2 × 10^-3 × 0.5
= -0.1 × 10^-3 T-m
Here, the negative sign shows that the potential decreases.
Page No 277:

Qstn #4
Figure (36-E1) shows some of the equipotential surfaces of the magnetic scalar potential. Find the magnetic field B at a point in the region.
Figure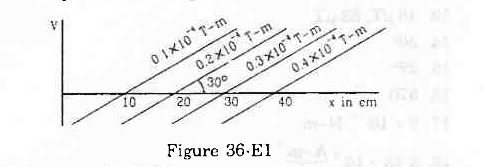
Ans : Given:
Perpendicular distance, dx = 10 sin30^ₒ cm = 0.05 m,
Change in the potential, dV = 0.1 × 10^-4 T-m
We know that the relation between the potential and the field is given by
`` B=-\frac{dV}{dx}``
`` \Rightarrow B=-\frac{0.1\times {10}^{-4}\,\mathrm{\,T\,}-m}{5\times {10}^{-2}m}``
`` \Rightarrow B=-2\times {10}^{-4}\,\mathrm{\,T\,}``
B is perpendicular to the equipotential surface. Here, it is at angle of 120° with the positive x-axis.
Page No 277:

Qstn #5
The magnetic field at a point, 10 cm away from a magnetic dipole, is found to be 2.0 × 10^-4 T. Find the magnetic moment of the dipole if the point is
Ans : Given:
Magnetic field strength, B = 2 × 10^-4 T
Distance of the point from the dipole, d = 10 cm = 0.1 m

#5-a
in end-on position of the dipole and
Ans : If the point is at the end-on position:
The magnetic field `` \left(B\right)`` on the axial point of the dipole is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{0}}{4\,\mathrm{\,\pi \,}}\frac{2M}{{d}^{3}}``
`` \,\mathrm{\,Here\,},M\,\mathrm{\,is\,}\,\mathrm{\,the\,}\,\mathrm{\,magnetic\,}\,\mathrm{\,moment\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,dipole\,}\,\mathrm{\,that\,}\,\mathrm{\,we\,}\,\mathrm{\,need\,}\,\mathrm{\,to\,}\,\mathrm{\,find\,}\,\mathrm{\,out\,}.``
`` \therefore 2\times {10}^{-4}=\frac{{10}^{-7}\times 2M}{{\left({10}^{-1}\right)}^{3}}``
`` \Rightarrow M=\frac{2\times {10}^{-4}\times {10}^{-3}}{{10}^{-7}\times 2}``
`` \Rightarrow M=1\,\mathrm{\,A\,}-{\,\mathrm{\,m\,}}^{2}``

#5-b
in broadside-on position of the dipole.
Ans : If the point is at broadside-on position (equatorial position):
The magnetic field `` \left(B\right)`` is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{0}}{4\,\mathrm{\,\pi \,}}\frac{\mathit{M}}{{\mathit{d}}^{\mathit{3}}}``
`` \Rightarrow 2\times {10}^{-4}=\frac{{10}^{-7}\times M}{{\left({10}^{-1}\right)}^{3}}``
`` \Rightarrow M=2\,\mathrm{\,A\,}-{\,\mathrm{\,m\,}}^{2}``
Page No 277:

Qstn #6
Show that the magnetic field at a point due to a magnetic dipole is perpendicular to the magnetic axis if the line joining the point with the centre of the dipole makes an angle of
tan-1 2with the magnetic axis.
Ans : Given:
Angle made by observation point P with the axis of the dipole, `` \theta `` = `` {\,\mathrm{\,tan\,}}^{-1}\left(\sqrt{2}\right)``
`` \Rightarrow \,\mathrm{\,tan\,}\theta =\sqrt{2}``
`` \Rightarrow 2={\,\mathrm{\,tan\,}}^{2}\theta ``
`` \Rightarrow \,\mathrm{\,tan\,}\theta =\,\mathrm{\,cot\,}\theta ``
`` \Rightarrow \frac{\,\mathrm{\,tan\,}\theta }{2}=\,\mathrm{\,cot\,}\theta ....\left(1\right)``
`` \,\mathrm{\,We\,}\,\mathrm{\,know\,},``
`` \frac{\,\mathrm{\,tan\,}\theta }{2}=\,\mathrm{\,tan\,}\alpha ....\left(2\right)``

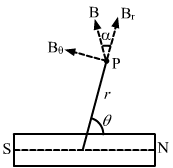
On comparing (1) and (2), we get
tan α = cot θ
`` \Rightarrow ``tan α = tan (90 - θ)
`` \Rightarrow ``α = 90 - θ
`` \Rightarrow ``θ + α = 90°
Hence, the magnetic field due to the dipole is perpendicular to the magnetic axis.
Page No 277:

Qstn #7
A bar magnet has a length of 8 cm. The magnetic field at a point at a distance 3 cm from the centre in the broadside-on position is found to be 4 × 10^-6 T. Find the pole strength of the magnet.
Ans : Given:
Length of the magnet, 2l = 8 cm = 8 `` \times `` 10^{`` -2``} m
Distance of the observation point from the centre of the dipole, d = 3 cm
Magnetic field in the broadside-on position, B = 4 × 10^-6 T
The magnetic field due to the dipole on the equatorial point `` \left(B\right)``is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{0}m2l}{4\,\mathrm{\,\pi \,}{\left({d}^{2}+{l}^{2}\right)}^{3/2}}``
`` ``
Here, m is the pole strength of the magnet.
On substituting the respective values, we get
`` 4\times {10}^{-6}=\frac{{10}^{-7}m\times 8\times {10}^{-2}}{{\left(9\times {10}^{-4}+16\times {10}^{-4}\right)}^{3/2}}``
`` \Rightarrow 4\times {10}^{-6}=\frac{m\times 8\times {10}^{-9}}{{\left(25\right)}^{3/2}\times {\left({10}^{-4}\right)}^{3/2}}``
`` \Rightarrow m=\frac{4\times {10}^{-6}\times 125\times {10}^{-6}}{8\times {10}^{-9}}``
`` \Rightarrow m=6.25\times {10}^{-2}\,\mathrm{\,A\,}-\,\mathrm{\,m\,}``
Thus, the pole strength of the magnet is 6.25`` \times ``10^{`` -2``}A-m.
Page No 277: