NEET-XII-Physics
36: Permanent Magnets
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #Section : ii
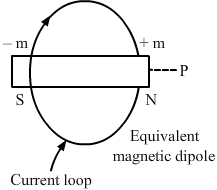
- Qstn #1A circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
(a) end-on position
(b) broadside-on position
(c) both
(d) nonedigAnsr: aAns : (a) end-on position
Points lying on the axis of a magnet are called end-on points. In our case, the point on the axis of the loop (on replacing the circular loop with an equivalent magnetic dipole) lies on the axis of the magnetic dipole or on the end-on position.
If P was the point on the axis of the loop, then it is clear from the figure that P lies on the end-on position of the equivalent magnetic dipole.
Page No 276:
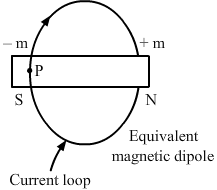
- Qstn #2A circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the loop is in
(a) end-on position
(b) broadside-on position
(c) both
(d) nonedigAnsr: bAns : (b) broadside-on position
The position of the points lying on the equator of a magnetic dipole is called the broadside-on position. In our case, the point on the loop (after replacement of the circular loop with an equivalent magnetic dipole) lies on the equatorial position of the equivalent magnetic dipole. Hence, the point lies on the broadside-on position.
If P was the point on the loop, then it is clear from the figure that point P lies on the broadside-on position of the equivalent magnetic dipole.
Page No 276:
- Qstn #3When a current in a circular loop is equivalently replaced by a magnetic dipole,
(a) the pole strength m of each pole is fixed
(b) the distance d between the poles is fixed
(c) the product md is fixed
(d) none of the abovedigAnsr: cAns : (c) the product md is fixed
When we replace a circular current-carrying loop with a magnetic dipole to resemble field lines of the circular loop, the pole strength m and the distance between the poles are not fixed.
But the magnetic dipole moment of both systems is always fixed. It is the product of the magnetic moment and the distance between the poles. In other words, md is fixed.
A current loop of area A and current I can be replaced with a magnetic dipole of dipole moment md.
i.e. md = IA
Page No 276:
- Qstn #4Let r be the distance of a point on the axis of a bar magnet from its centre. The magnetic field at such a point is proportional to
(a)
1r
(b)
1r2
(c)
1r3
(d) none of thesedigAnsr: dAns : (d) None of these
Magnetic field B due to a bar magnet of magnetic moment M at distance r of the point on the axis of the magnet from its centre is given by
`` B=\frac{{\mu }_{o}}{4\pi }\frac{2Mr}{{\left({r}^{2}-{l}^{2}\right)}^{2}}``
Here, 2l is the length of the magnet.
So, from the above formula, it can be easily seen that `` B\propto \frac{r}{{\left({r}^{2}-{l}^{2}\right)}^{2}}``.
Page No 276:
- Qstn #5Let r be the distance of a point on the axis of a magnetic dipole from its centre. The magnetic field at such a point is proportional to
(a)
1r
(b)
1r2
(c)
1r3
(d) none of thesedigAnsr: cAns : (c) `` \frac{1}{{r}^{3}}``
Magnetic field B due to a bar magnet of magnetic moment M at distance r of the point on the axis from its centre is given by
`` B=\frac{{\mu }_{\mathit{0}}2Mr}{4\,\mathrm{\,\pi \,}{\left({r}^{2}-{l}^{2}\right)}^{2}}``
Here, 2l is the length of the magnet.
When the distance of the point where the magnetic field has to be calculated is greater than the length of the magnet, i.e `` r>>l``, the bar magnet acts like a magnetic dipole whose magnetic field is
B`` \propto \frac{1}{{r}^{3}}``
Now, l in the denominator can be neglected.
So, the correct option is
(c).
Page No 276:
- Qstn #6Two short magnets of equal dipole moments M are fastened perpendicularly at their centre (figure 36-Q1). The magnitude of the magnetic field at a distance d from the centre on the bisector of the right angle is
(a)
μ04πMd3
(b)
μ04π2 Md3
(c)
μ04π22Md3
(d)
μ04π2Md3Figure digAnsr: cAns : (c) `` \frac{{\mu }_{0}}{4\pi }\frac{2\sqrt{2}M}{{d}^{3}}``
digAnsr: cAns : (c) `` \frac{{\mu }_{0}}{4\pi }\frac{2\sqrt{2}M}{{d}^{3}}``
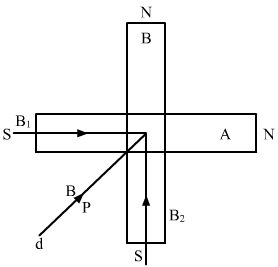
Magnetic field (B1) due to the short dipole A of dipole moment M at an axial point is given by,
`` {\stackrel{\to }{B}}_{1}=\frac{{\mu }_{0}}{4\,\mathrm{\,\pi \,}}\frac{2M}{{d}^{3}}...\left(1\right)``
Magnetic field (B2) due to the short dipole B of dipole moment M at an axial point is given by,
`` {\stackrel{\to }{B}}_{2}=\frac{{\mu }_{0}}{4\,\mathrm{\,\pi \,}}\frac{2M}{{d}^{3}}...\left(2\right)``
Resultant magnetic field (B) will be,
B = `` \sqrt{{{B}_{1}}^{2}+{{B}_{2}}^{2}}``
B = `` \frac{{\mu }_{0}}{4\,\mathrm{\,\pi \,}}\frac{2\sqrt{2}M}{{d}^{3}}``
Page No 276:
- Qstn #7Magnetic meridian is
(a) a point
(b) a line along north-south
(c) a horizontal plane
(d) a vertical planedigAnsr: dAns : (d) a vertical plane
Magnetic meridian at a place is not a line but a vertical plane passing through the axis of a freely suspended magnet.
Page No 276:
- Qstn #8A compass needle which is allowed to move in a horizontal plane is taken to a geomagnetic pole. It
(a) will stay in north-south direction only
(b) will stay in east-west direction only
(c) will become rigid showing no movement
(d) will stay in any positiondigAnsr: dAns : (d) will stay in any position
When taken to a geomagnetic pole, a compass needle that is allowed to move in a horizontal plane will try to suspend itself vertically to the horizontal plane containing the compass. In other words, the horizontal plane containing the compass will restrict the compass to suspend itself in vertical direction; hence, the compass will stay in any position.
However, a freely suspended magnet will become vertical at poles, with its north pole pointing towards Earth at its north pole (which is magnetic south).
Page No 276:
- Qstn #9A dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
(a) in horizontal direction only
(b) in vertical direction only
(c) in any direction except vertical and horizontal
(d) in the direction it is releaseddigAnsr: dAns : (d) in the direction it is released
At the geomagnetic equator, the needle tries to suspend itself in horizontal direction. But here the needle is restricted to move only in the vertical plane perpendicular to the magnetic meridian. Hence, the needle will stay in the direction it is released.
Page No 276:
- Qstn #10Which of the following four graphs may best represent the current-deflection relation in a tangent galvanometer?
FigureAns : (c) curve
Since i `` \propto `` tan `` \theta ``, the only graph that represents this correlation is curve c.
Page No 276:
- Qstn #11A tangent galvanometer is connected directly to an ideal battery. If the number of turns in the coil is doubled the deflection will
(a) increase
(b) decrease
(c) remain unchanged
(d) either increase or decreasedigAnsr: cAns : (c) remain unchanged
For a tangent galvanometer, deflection is given by
`` \theta ={\,\mathrm{\,tan\,}}^{-1}\left(\frac{i}{k}\right)``
Here, k is the constant called reduction factor.
From the above formula, we can say that deflection is independent of the number of turns.
Hence, on doubling the number of turns, deflection remains the same.
Page No 276:
- Qstn #12If the current is doubled, the deflection is also doubled in
(a) a tangent galvanometer
(b) a moving-coil galvanometer
(c) both
(d) nonedigAnsr: bAns : (b) a moving coil galvanometer
The current and deflection dependence of a moving coil galvanometer is given by
`` i=\frac{k}{nAB}\theta \Rightarrow i\propto \theta ``
Therefore, if we double the current, the deflection also gets doubled.
However, in a tangent galvanometer, `` i\propto \,\mathrm{\,tan\,}\theta ``; that is, there is no direct relation between `` \theta `` and current.
Hence, the correct option is
(b).
Page No 276:
- Qstn #13A very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying as electric current i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
(a) very nearly 2πaiB perpendicular to the plane of the wire
(b) 2πaiB in the plane of the wire
(c) πaiB along the magnet
(d) zerodigAnsr: aAns : (a) very nearly 2`` \,\mathrm{\,\pi \,}``aiB perpendicular to the plane of the wire
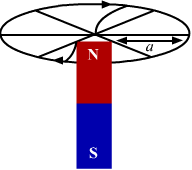
In this case, the north pole of the magnet is coinciding with the centre of the circular loop carrying electric current i. So, the magnetic field lines almost lie on the plane of the ring and the force due to the field lines is perpendicular to the field lines and to the plane of the circular ring.
Let idl be the current element, B be the magnetic field and dF be the force on the current element idl.
Now
dF = Bidl `` \Rightarrow F={\int }_{0}^{2\,\mathrm{\,\pi a\,}}\,\mathrm{\,B\,}idl``
`` \Rightarrow F=2\,\mathrm{\,\pi a\,}i\,\mathrm{\,B\,}``
Thus, the force acting on the wire is 2`` \,\mathrm{\,\pi \,}``aiB and it is perpendicular to the plane of the wire.
Page No 277:
- #Section : iii