NEET-XII-Physics
33: Thermal and Chemical Effects of Electric Current
- #2Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
FigureAns :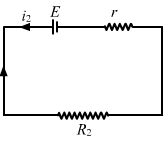
For the given time t, let the currents passing through the resistance R1 and R2 be i1 and i2 , respectively.
Applying Kirchoff's Voltage Law to circuit-1, we get:
`` \epsilon -{i}_{1}r-{i}_{1}{R}_{1}=0``
`` \Rightarrow {i}_{1}=\frac{\epsilon }{r+{R}_{1}}``
Similarly, the current in the other circuit,
`` {i}_{2}=\frac{\epsilon }{r+{R}_{2}}``
The thermal energies through the resistances are given by
`` {i}_{1}^{2}{R}_{1}t={i}_{2}^{2}{R}_{2}t``
`` {\left(\frac{\epsilon }{r+{R}_{1}}\right)}^{2}{R}_{1}t={\left(\frac{\epsilon }{r+{R}_{2}}\right)}^{2}{R}_{2}t``
`` \frac{{R}_{1}}{{\left(r+{R}_{1}\right)}^{2}}=\frac{{R}_{2}}{{\left(r+{R}_{2}\right)}^{2}}``
`` \frac{\left({r}^{2}+{{R}_{1}}^{2}+2r{R}_{1}\right)}{{R}_{1}}=\frac{\left({r}^{2}+{{R}_{2}}^{2}+2r{R}_{2}\right)}{{R}_{2}}``
`` \frac{{r}^{2}}{{R}_{1}}+{R}_{1}=\frac{{r}^{2}}{{R}_{2}}+{R}_{2}``
`` {r}^{2}\left(\frac{1}{{R}_{1}}-\frac{1}{{R}_{2}}\right)={R}_{2}-{R}_{1}``
`` {r}^{2}\times \frac{{R}_{2}-{R}_{1}}{{R}_{1}{R}_{2}}={R}_{2}-{R}_{1}``
`` {r}^{2}={R}_{1}{R}_{2}``
`` \Rightarrow r=\sqrt{{R}_{1}{R}_{2}}``
Page No 217: