NEET-XII-Physics
33: Thermal and Chemical Effects of Electric Current
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #Section : i
- Qstn #1If a constant potential difference is applied across a bulb, the current slightly decreases as time passes and then becomes constant. Explain.Ans : As a constant potential difference is applied across a bulb, due to Joule's heating effect, the temperature of the bulb increases. As the temperature of the bulb filament increases, its resistance also increases, as resistance R is the function of temperature T. It is given by R = R0(1+αT). With an increase in the value of resistance, the value of current decreases as `` i=\frac{V}{R}``. Now, the heat generated by the resistance is constantly radiated to the surroundings. Thus, the value of its temperature is maintained and hence its resistance. As a result, current through the bulb filament becomes constant.
Page No 217:
- Qstn #2Two unequal resistances, R1 and R2, are connected across two identical batteries of emf ε and internal resistance r (figure). Can the thermal energies developed in R1 and R2 be equal in a given time? If yes, what will be the condition?
FigureAns :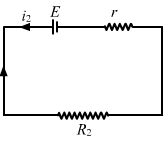
For the given time t, let the currents passing through the resistance R1 and R2 be i1 and i2 , respectively.
Applying Kirchoff's Voltage Law to circuit-1, we get:
`` \epsilon -{i}_{1}r-{i}_{1}{R}_{1}=0``
`` \Rightarrow {i}_{1}=\frac{\epsilon }{r+{R}_{1}}``
Similarly, the current in the other circuit,
`` {i}_{2}=\frac{\epsilon }{r+{R}_{2}}``
The thermal energies through the resistances are given by
`` {i}_{1}^{2}{R}_{1}t={i}_{2}^{2}{R}_{2}t``
`` {\left(\frac{\epsilon }{r+{R}_{1}}\right)}^{2}{R}_{1}t={\left(\frac{\epsilon }{r+{R}_{2}}\right)}^{2}{R}_{2}t``
`` \frac{{R}_{1}}{{\left(r+{R}_{1}\right)}^{2}}=\frac{{R}_{2}}{{\left(r+{R}_{2}\right)}^{2}}``
`` \frac{\left({r}^{2}+{{R}_{1}}^{2}+2r{R}_{1}\right)}{{R}_{1}}=\frac{\left({r}^{2}+{{R}_{2}}^{2}+2r{R}_{2}\right)}{{R}_{2}}``
`` \frac{{r}^{2}}{{R}_{1}}+{R}_{1}=\frac{{r}^{2}}{{R}_{2}}+{R}_{2}``
`` {r}^{2}\left(\frac{1}{{R}_{1}}-\frac{1}{{R}_{2}}\right)={R}_{2}-{R}_{1}``
`` {r}^{2}\times \frac{{R}_{2}-{R}_{1}}{{R}_{1}{R}_{2}}={R}_{2}-{R}_{1}``
`` {r}^{2}={R}_{1}{R}_{2}``
`` \Rightarrow r=\sqrt{{R}_{1}{R}_{2}}``
Page No 217:
- Qstn #3When a current passes through a resistor, its temperature increases. Is it an adiabatic process?Ans : No, the rise in the temperature of a resistor on passing current through it is not an adiabatic process. In an adiabatic process, there is no heat exchange between the system and the surroundings. Here, some part of Joule's heat developed inside the resistor increases the temperature of the resistor and the remaining part is dissipated in the surroundings. Thus, the given process cannot be adiabatic.
Page No 217:
- Qstn #4Apply the first law of thermodynamics to a resistor carrying a current i. Identify which of the quantities &traingle;Q, &traingle;U and &traingle;W are zero, positive and negative.Ans : The battery is doing positive work on a resistor carrying current i. Thus, ∆W is positive. The work done on the resistor is used to increase its thermal energy; thus ∆Q is positive. As the temperature of the resistor rises, ∆U is positive.
Page No 217:
- Qstn #5Do all thermocouples have a neutral temperature?Ans : The temperature of the hot junction at which the thermo-emf in a thermocouple becomes maximum is called neutral temperature for that thermocouple. For a thermocouple in which the constants a and b have the same sign, the neutral temperature will be less than the temperature of the cold junction of the thermocouple (as `` {\theta }_{n}=-\frac{a}{b}``).
There will be no neutral or inversion temperature, as the temperature of the hot junction cannot be less than the temperature of the cold junction.
Page No 217:
- Qstn #6Is inversion temperature always double the neutral temperature? Does the unit of temperature have an effect in deciding this question?Ans : If the inversion temperature and neutral temperature are measured in degree Celsius, then it is correct to say that "inversion temperature is always double the neutral temperature." When temperature is measured in other units, such as Kelvin, then inversion temperature is not the double of neutral temperature.
Page No 217:
- Qstn #7Is neutral temperature always the arithmetic mean of the inversion temperature and the temperature of the cold junction? Does the unit of temperature have an effect in deciding this question?Ans : No, the neutral temperature is not always the arithmetic mean of the inversion temperature and the temperature of the cold junction. That is valid only when the unit of temperature is degree Celsius.
Page No 217:
- Qstn #8Do the electrodes in an electrolytic cell have fixed polarity like a battery?Ans : No, the electrodes in an electrolytic cell do not have fixed polarity like that of a battery. If we take an electrolytic cell consisting of the Ag electrodes and the AgNO3 as electrolyte. When the battery is connected to it, the end to which the positive terminal of the battery is connected is the anode and the end to which the negative terminal is connected is the cathode. `` {\,\mathrm{\,NO\,}}_{3}^{-}`` ions are deposited at the anode and Ag+ ions are deposited at the cathode. When the connection of the electrolytic cell is reversed, the polarities of the electrodes are also reversed.
Page No 217:
- Qstn #9As temperature increases, the viscosity of liquids decreases considerably. Will this decrease the resistance of an electrolyte as the temperature increases?Ans : Yes, the resistance of the electrolyte will decrease with an increase in temperature. This is because when the temperature of an electrolytic solution increases, its viscosity decreases and mobility of the ions in the solution increases.
Page No 217:
- #Section : ii
- Qstn #1Which of the following plots may represent the thermal energy produced in a resistor in a given time as a function of the electric current?
FigureAns : Plot
(a) is the correct option.
When current passes through a resistor, the heat produced,
H = I2Rt,
where I = current
R = resistance of the resistor
t = time for which current is flowing
This relation shows that the heat produced for a given time in a resistor varies with the square of current flowing through it. Hence, the plot between H vs I should be a parabola symmetric along the H axis, which is represented by curve
a.
Page No 217:
- Qstn #2A constant current i is passed through a resistor. Taking the temperature coefficient of resistance into account, indicate which of the plots shown in the figure best represents the rate of production of thermal energy in the resistor.
FigureAns : Plot
(d) is correct.
When current passes through a resistor, the temperature of the resistor increases due to the heat produced in it.
H = i2Rt,
where i = current flowing through the resistor
R = resistance of the resistor
t = time for which the current is flowing
With the increase in the temperature of the resistor, its resistance is also increased. The rate of production of thermal energy in the resistor of the circuit is given by the following relation:
`` \frac{dU}{dt}=\frac{d}{dt}\left({i}^{2}Rt\right)={i}^{2}R``,
where i = current flowing through the resistor
R = resistance of the resistor
Rate of production of thermal energy in the resistor is directly proportional to the resistance. So, due to increase in resistance, `` \frac{dU}{dt}`` also increases linearly, which is best represented by plot d.
Page No 218:
- Qstn #3Consider the following statements regarding a thermocouple.
(A) The neutral temperature does not depend on the temperature of the cold junction.
(B) The inversion temperature does not depend on the temperature of the cold junction.
(a) A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) A and B are wrong.digAnsr: bAns : (b) A is correct but B is wrong.
The value of neutral temperature is constant for a thermocouple. It depends on the nature of materials and is independent of the temperature of the cold junction. Inversion temperature depends on the temperature of the cold junction, as well as the nature of the material.
Page No 218: