HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

33: Thermal and Chemical Effects of Electric Current

with Solutions - page 4
Qstn# iv-12 Prvs-QstnNext-Qstn
  • #12
    The 2.0 Ω resistor shown in the figure is dipped into a calorimeter containing water. The heat capacity of the calorimeter together with water is 2000 J K-1. (a) If the circuit is active for 15 minutes, what would be the rise in the temperature of the water? (b) Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?
    Figure
    Ans : The effective resistance of the circuit,
    `` {\,\mathrm{\,R\,}}_{eff}=\left(\frac{6\times 2}{6+2}\right)+1=\frac{5}{2}\,\mathrm{\,A\,}``
    `` ``
    `` ``
    Current i through the circuit,
    `` i=\frac{V}{{R}_{eff}}=\frac{6}{5/2}=\frac{12}{5}\,\mathrm{\,A\,}``

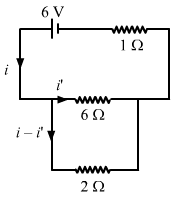
    Let i' be the current through the 6 Ω resistor. Then,
    i' × 6 = (i - i') × 2
    `` \Rightarrow 6i\text{'}=\left(\frac{12}{5}\right)\times 2-2i\text{'}``
    `` \Rightarrow 8i\text{'}=\frac{24}{5}``
    `` \Rightarrow i\text{'}=\frac{24}{(5\times 8)}=\frac{3}{5}\,\mathrm{\,A\,}``
    `` \Rightarrow i-i\text{'}=\frac{12}{5}-\frac{3}{5}=\frac{9}{5}\,\mathrm{\,A\,}`` (a) Heat generated in the 2 Ω resistor,
    H = (i - i')2Rt
    `` \Rightarrow H=\left(\frac{9}{5}\right)\times \left(\frac{9}{5}\right)\times 2\times 15\times 60=5832\,\mathrm{\,J\,}``
    The heat capacity of the calorimeter together with water is 2000 J K-1. Thus, 2000 J of heat raise the temp by 1 K.
    ∴ 5832 J of heat raises the temperature by `` \frac{5832}{2000}`` = 2.916 K (b) When the 6 Ω resistor gets burnt, the effective resistance of the circuit,
    Reff = 1 + 2 = 3 Ω
    Current through the circuit,
    i = `` \frac{6}{3}`` = 2 A
    Heat generated in the 2 Ω resistor = (2)2× 2 × 15 × 60 = 7200 J
    2000 J raise the temperature by 1 K.
    ∴ 7200 J raise the temperature by `` \frac{7200}{2000}`` = 3.6 K .
    Page No 219:
  • #12-a
    If the circuit is active for 15 minutes, what would be the rise in the temperature of the water?
    Ans : Heat generated in the 2 Ω resistor,
    H = (i - i')2Rt
    `` \Rightarrow H=\left(\frac{9}{5}\right)\times \left(\frac{9}{5}\right)\times 2\times 15\times 60=5832\,\mathrm{\,J\,}``
    The heat capacity of the calorimeter together with water is 2000 J K-1. Thus, 2000 J of heat raise the temp by 1 K.
    ∴ 5832 J of heat raises the temperature by `` \frac{5832}{2000}`` = 2.916 K
  • #12-b
    Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?
    Figure
    Ans : When the 6 Ω resistor gets burnt, the effective resistance of the circuit,
    Reff = 1 + 2 = 3 Ω
    Current through the circuit,
    i = `` \frac{6}{3}`` = 2 A
    Heat generated in the 2 Ω resistor = (2)2× 2 × 15 × 60 = 7200 J
    2000 J raise the temperature by 1 K.
    ∴ 7200 J raise the temperature by `` \frac{7200}{2000}`` = 3.6 K .
    Page No 219: