NEET-XII-Physics
32: Electric Current in Conductors
- #36Find the potential difference Va - Vb in the circuits shown in the figure (32-E12).
figure 32-12 Ans :
Ans :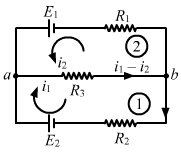
Applying KVL in loop 1, we get:
`` {i}_{1}{R}_{2}-{E}_{2}+\left({i}_{1}+{i}_{2}\right){R}_{3}=0``
`` ({R}_{2}+{R}_{3}){i}_{1}+{R}_{3}{i}_{2}={E}_{2}...\left(1\right)``
Applying KVL in loop 2, we get:
`` {i}_{2}{R}_{1}-{E}_{1}+\left({i}_{1}+{i}_{2}\right){R}_{3}=0``
`` \left({R}_{1}+{R}_{3}\right){i}_{2}+{R}_{3}{i}_{1}={E}_{1}...\left(2\right)``
Multiplying equation (1) by (R1+R3) and (2) by R3 and then subtracting (2) from (1), we get:
`` {i}_{1}=\frac{{E}_{2}\left({R}_{1}+{R}_{3}\right)-{E}_{1}{R}_{3}}{\left({R}_{1}{R}_{2}+{R}_{2}{R}_{3}+{R}_{3}{R}_{1}\right)}``
Similarly, multiplying equation (1) by R3 and (2) by (R1+R3), and then subtracting (2) from (1), we get:
`` {i}_{2}=\frac{{E}_{1}\left({R}_{2}+{R}_{3}\right)-{E}_{2}{R}_{3}}{\left({R}_{1}{R}_{2}+{R}_{2}{R}_{3}+{R}_{3}{R}_{1}\right)}``
From the figure,
`` {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=\left({i}_{1}+{i}_{2}\right){R}_{3}``
`` \Rightarrow {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=\left[\frac{{E}_{1}{R}_{2}+{E}_{2}{R}_{1}}{\left({R}_{1}{R}_{2}+{R}_{2}{R}_{3}+{R}_{3}{R}_{1}\right)}\right]{R}_{3}``
`` \Rightarrow {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=\frac{{\displaystyle \frac{{E}_{1}}{{R}_{1}}}+{\displaystyle \frac{{E}_{2}}{{R}_{2}}}}{{\displaystyle \frac{1}{{R}_{1}}}+{\displaystyle \frac{1}{{R}_{2}}}+{\displaystyle \frac{1}{{R}_{3}}}}``
(b) The circuit in figure b can be redrawn as shown below:
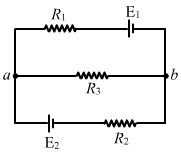
We can see that it is similar to the circuit in figure a and, hence, the answer obtained will be same.
Page No 200: