NEET-XII-Physics
32: Electric Current in Conductors
- #34Figure (32-E10) shows a part of an electric circuit. The potentials at the points a, b and c are 30 V, 12 V and 2 V respectively. Find the currents through the three resistors.
Figure 32-E10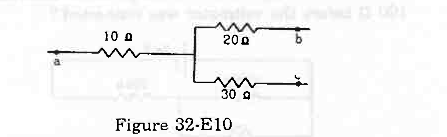 Ans :
Ans :
Let the potential at the point o be X volts.
From the figure,
`` {i}_{1}=\frac{{V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,o\,}}}{10}``
`` {V}_{\,\mathrm{\,a\,}}=30\,\mathrm{\,V\,}\,\mathrm{\,and\,}{V}_{\,\mathrm{\,o\,}}=X``
`` So,{i}_{1}=\frac{30-X}{10}``
`` \,\mathrm{\,Similarly\,},``
`` {i}_{2}=\frac{{V}_{\,\mathrm{\,o\,}}-{V}_{\,\mathrm{\,b\,}}}{20}``
`` =\frac{X-12}{20}``
`` \,\mathrm{\,And\,}``
`` {i}_{3}=\frac{{V}_{\,\mathrm{\,o\,}}-{V}_{\,\mathrm{\,c\,}}}{30}``
`` =\frac{X-2}{30}``
Also, from kirchoff's junction law we have:
i1 = i2 + i3
`` \Rightarrow \frac{30-X}{10}=\frac{X-12}{20}+\frac{X-2}{30}``
`` \Rightarrow 30-X=\frac{X-12}{2}+\frac{X-2}{3}``
`` \Rightarrow 30-X=\frac{3X-36+2X-4}{6}``
`` \Rightarrow 180-6X=5X-40``
`` \Rightarrow 11X=220``
`` \Rightarrow X=\frac{220}{11}=20\,\mathrm{\,V\,}``
Thus, the currents through the three resistors are:
`` {i}_{1}=\frac{30-20}{10}=1\,\mathrm{\,A\,}``
`` {i}_{2}=\frac{20-12}{20}=\frac{8}{20}=0.4\,\mathrm{\,A\,}``
`` {i}_{3}=\frac{20-2}{30}=\frac{18}{30}=0.6\,\mathrm{\,A\,}``
Page No 200: