32: Electric Current In Conductors : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

32: Electric Current in Conductors

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #9
A capacitor C₁ of capacitance 1 μF and a capacitor C₂ of capacitance 2 μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t = 0.
(a) The current in each of the two discharging circuits is zero at t = 0.
(b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(c) The currents in the two discharging circuits at t = 0 are unequal.
(d) C₁ loses 50% of its initial charge sooner than C₂ loses 50% of its initial charge.
digAnsr: b,d,V
Ans : (b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(d) C₁ loses 50% of its initial charge sooner than C₂ loses 50% of its initial charge.
Let the voltage of the battery connected to the capacitors be V. Both the capacitors will charge up to the same potential (V).
The charge on the capacitors C₁is C₁V = (1 μF)×V
The charge on the capacitors C₂is C₂V = (2 μF)×V
The charge on the discharging circuit at an instant t,
`` Q=CV{e}^{-t/RC}``
The current through the discharging circuit,
`` \frac{\,\mathrm{\,d\,}Q}{\,\mathrm{\,d\,}t}=-\frac{CV}{RC}{\,\mathrm{\,e\,}}^{-t/RC}=\frac{\mathit{V}}{\mathit{R}}{\,\mathrm{\,e\,}}^{-\,\mathrm{\,t\,}/\,\mathrm{\,R\,}\,\mathrm{\,C\,}}``
At t = 0, the current through the discharging circuit will be `` \frac{V}{R}`` for both the capacitors.
Let the time taken by the capacitor C₁ to lose 50% of the charge be t₁.
`` {Q}_{1}=\frac{{C}_{1}V}{2}``
`` \frac{{C}_{1}V}{2}={C}_{1}V{e}^{-{t}_{1}/RC}``
`` \frac{1}{2}={e}^{-{t}_{1}/RC}``
Taking natural log on both sides, we get:
`` -\,\mathrm{\,ln\,}2=-\frac{{t}_{1}}{R{C}_{1}}``
`` {t}_{1}=R{C}_{1}\,\mathrm{\,ln\,}2``
Similarly,
Time taken for capacitor C₂: `` {t}_{2}=R{C}_{2}\,\mathrm{\,ln\,}2``
As, C₁ < C₂, t₁ < t₂
Thus, we can say that C₁ loses 50% of its initial charge sooner than C₂ loses 50% of its initial charge.
Page No 198:

#
Section : iv

Qstn #1
The amount of charge that passes in time t through a cross-section of a wire is
Q(t) = At² + Bt + C.

#1-a
Write the dimensional formulae for A, B and C.
Ans : Amount of charge,
Q(t) = At² + Bt + C
We can only add the terms with the same dimensions. So, all the individual terms will have dimensions equal to the dimensions of the charge.
Comparing the dimensions of each term separately, we get:
`` A{t}^{2}=Q``
`` \Rightarrow A=\frac{Q}{{t}^{2}}``
`` Q=It``
`` \Rightarrow A=\frac{I}{t}=\left[{\,\mathrm{\,AT\,}}^{-1}\right],``
where I = current through the wire
Now,
`` Bt=Q``
`` \Rightarrow B=\frac{Q}{t}=I=\left[\,\mathrm{\,A\,}\right]``
Also,
`` C=Q``
`` \Rightarrow C=\left[\,\mathrm{\,AT\,}\right]``

#1-b
If the numerical values of A, B and C are 5, 3 and 1, respectively, in S.I units, find the value of the current at t = 5 s.
Ans : Current I = rate of flow of charge
`` \Rightarrow I=\frac{\,\mathrm{\,d\,}Q}{\,\mathrm{\,d\,}t}=\frac{\,\mathrm{\,d\,}}{\,\mathrm{\,d\,}t}\left(A{t}^{2}+Bt+C\right)``
`` \Rightarrow I=2At+B``
`` A=5,B=3\,\mathrm{\,and\,}t=5\,\mathrm{\,s\,}``
`` \Rightarrow I=2\times 5\times 5+3=53\,\mathrm{\,A\,}``
Page No 198:

Qstn #2
An electron gun emits 2.0 ×10¹⁶ electrons per second. What electric current does this correspond to?
Ans : Rate of emission of electrons = 2 ×10¹⁶ per second
Total charge passing through the gun = 2 ×10¹⁶ ×1.6 × 10^-19= 3.2 × 10^-3 per second
We know:
Current, I = rate of flow of charge
∴ I = 3.2 × 10^-3 A
Page No 198:

Qstn #3
The electric current existing in a discharge tube is 2.0 μA. How much charge is transferred across a cross-section of the tube in 5 minutes?
Ans : Let Q amount of charge be transferred across the cross-section of the tube.
Given:
Current through the discharge tube, I = 2 μA = 2 × 10^-6 A
Time taken to transfer charge, t = 5 mins = 300 s
We know:
Q = It
∴ Q = 2 × 10^-6 × 300 = 6× 10^-4 C
Page No 198:

Qstn #4
The current through a wire depends on time as i = i₀ + αt,
where i₀ = 10 A and α = 4 As^-1. Find the charge that crosses through a section of the wire in 10 seconds.
Ans : Current through the wire varies with time as
i = i₀+ α t
Time interval, t = 10 s
i₀ = 10 A
α = 4 A/sec
We know that for variable current,
`` q={\int }_{0}^{t}i\,\mathrm{\,d\,}t``
`` \Rightarrow q={\int }_{0}^{t}\left({i}_{0}+\alpha t\right)\,\mathrm{\,d\,}t``
`` \Rightarrow q={i}_{0}t+\frac{\alpha {t}^{2}}{2}``
`` \therefore q=10\times 10+4\times \frac{{\left(10\right)}^{2}}{2}``
`` =100+200``
`` =300\,\mathrm{\,C\,}``
Page No 198:

Qstn #5
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm². Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m^-3.
Ans : Given:
Current, i = 1 A
Area of cross-section, A = 1 mm² = 1 × 10^-6 m²
Density of copper, `` \rho `` = 9000 kg/m³
Length of the conductor = l
Also,
Mass of copper wire = Volume × density
`` \Rightarrow m\mathit{=}A\times l\times \rho ``
`` \mathit{\Rightarrow }m\mathit{=}A\times l\times 9000\,\mathrm{\,kg\,}``
We know that the number of atoms in molecular mass M = N_A
∴ Number of atoms in mass m, N = `` \left(\frac{{\,\mathrm{\,N\,}}_{\,\mathrm{\,A\,}}}{M}\right)m``,
where N_Ais known as Avagadro's number and is equal to 6 × 10²³ atoms.
`` \Rightarrow N=\left(\frac{{\,\mathrm{\,N\,}}_{\,\mathrm{\,A\,}}}{\,\mathrm{\,M\,}}\right)m``
`` \Rightarrow N=\left(\frac{{\,\mathrm{\,N\,}}_{\,\mathrm{\,A\,}}}{\,\mathrm{\,M\,}}\right)\times A\times l\times 9000``
`` ``
Also, it is given that
No. of free electrons = No. of atoms
Let n be the number of free electrons per unit volume
`` n=\frac{\,\mathrm{\,Number\,}\,\mathrm{\,of\,}\,\mathrm{\,electrons\,}}{\,\mathrm{\,Volume\,}}``
`` =\frac{{\,\mathrm{\,N\,}}_{\,\mathrm{\,A\,}}\times A\times l\times 9000}{M\times A\times l}``
`` =\frac{{\,\mathrm{\,N\,}}_{\,\mathrm{\,A\,}}\times 9000}{M}``
`` =\frac{6\times {10}^{23}\times 9000}{63.5\times {10}^{-3}}``
`` \therefore i\mathit{=}{V}_{\,\mathrm{\,d\,}}nAe``
`` \Rightarrow {V}_{d}=\frac{1}{{\displaystyle \frac{6\times {10}^{23}\times 9000}{63.5\times {10}^{-3}}\times {10}^{-6}\times 1.6\times {10}^{-19}}}``
`` =\frac{63.5\times {10}^{-3}}{6\times {10}^{23}\times 9000\times {10}^{-6}\times 1.6\times {10}^{-19}}``
`` =\frac{63.5\times {10}^{-3}}{6\times {10}^{26}\times 9\times {10}^{-6}\times 1.6\times {10}^{-19}}``
`` =\frac{63.5\times {10}^{-3}}{6\times 9\times 16}``
`` =0.073\times {10}^{-3}\,\mathrm{\,m\,}/\,\mathrm{\,s\,}``
`` =0.073\,\mathrm{\,mm\,}/\,\mathrm{\,s\,}``
Page No 198:

Qstn #6
A wire of length 1 m and radius 0.1 mm has a resistance of 100 Ω. Find the resistivity of the material.
Ans : Let ρ be the resistivity of the wire.
Given:
Length, l = 1 m
Radius, r = 0.1 × 10^-3 m
Area, A = `` \,\mathrm{\,\pi \,}{r}^{2}``
Resistance, R = 1000 Ω
We know:
`` R=\rho \frac{l}{A}``
`` \Rightarrow \rho =\frac{RA}{l}``
`` =\frac{1000\times \,\mathrm{\,\pi \,}\times 0.1\times 0.1\times {10}^{-6}}{1}``
`` =\,\mathrm{\,\pi \,}\times {10}^{-6}\,\mathrm{\,\Omega m\,}``
Page No 198:

Qstn #7
A uniform wire of resistance 100 Ω is melted and recast as a wire whose length is double that of the original. What would be the resistance of the wire?
Ans : Let
Resistivity of the wire = ρ
Original length of the wire = l
New length of the wire = l'
Original area of the wire = A
New area of the wire = A'
Original resistance of the wire = R = 100 Ω
New resistance of the wire = R'
Given:
l' = 2l
The volume of the wire remains constant. So,
`` Al=A\text{'}l\text{'}``
`` \Rightarrow A\text{'}=\frac{A}{2}``
We know:
`` R=\frac{\rho l}{A}``
`` \Rightarrow R\text{'}=\frac{\rho l\text{'}}{A\text{'}}``
`` \Rightarrow \frac{R\text{'}}{R}=\frac{l\text{'}A}{lA\text{'}}``
`` \because l\text{'}=2l,A\text{'}=\frac{A}{2}``
`` \Rightarrow \frac{R\text{'}}{R}=\frac{\left(2l\right)A}{l\left({\displaystyle \frac{A}{2}}\right)}=4``
`` \Rightarrow R\text{'}=4R=400\,\mathrm{\,\Omega \,}``
Page No 198:

Qstn #8
Consider a wire of length 4 m and cross-sectional area 1 mm² carrying a current of 2 A. If each cubic metre of the material contains 10²⁹free electrons, find the average time taken by an electron to cross the length of the wire.
Ans : Given:
Current through the wire, i = 2 A
Length of the wire, l = 4 m
Area of cross section, A = 1 mm² = 1 × 10^-6 m²
Number of electrons per unit volume, n = 10²⁹
We know:
`` i=nA{V}_{d}e``
`` \Rightarrow {V}_{d}=\frac{i}{nAe}``
`` =\frac{2}{{10}^{29}\times {10}^{-6}\times 1.6\times {10}^{-19}}``
`` \Rightarrow {V}_{\,\mathrm{\,d\,}}=\frac{1}{8000}\,\mathrm{\,m\,}/\,\mathrm{\,s\,},``
where V_d is the drift speed.
Let t be the time taken by an electron to cross the length of the wire.
`` \Rightarrow t=\frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\text{the}\,\mathrm{\,wire\,}}{\text{D}\,\mathrm{\,rift\,}\,\mathrm{\,speed\,}}``
`` =\frac{l}{{V}_{\,\mathrm{\,d\,}}}``
`` \therefore t=\frac{4}{{\displaystyle \frac{1}{8000}}}``
`` =32\times {10}^{3}\,\mathrm{\,s\,}``
Page No 198:

Qstn #9
What length of a copper wire of cross-sectional area 0.01 mm² will be needed to prepare a resistance of 1 kΩ? Resistivity of copper = 1.7 × 10^-8 Ωm
Ans : Given:
Resistivity of copper, ρ_cu= 1.7 × 10^-8 Ωm
Area of cross-section, A = 0.01 mm²= 0.01 × 10^-6 m²
Required resistance, R = 1 kΩ = 10³ Ω
Let l be the required length of the copper wire.
We know:
`` R=\frac{\rho l}{A}``
`` \Rightarrow l=\frac{RA}{{\rho }_{\,\mathrm{\,cu\,}}}``
`` \Rightarrow l=\frac{{10}^{3}\times 0.01\times {10}^{-6}}{1.7\times {10}^{-8}}``
`` \therefore l=0.58\times {10}^{3}\,\mathrm{\,m\,}=0.6\,\mathrm{\,km\,}``
Page No 198:

Qstn #10
Figure (32.E1) shows a conductor of length l with a circular cross-section. The radius of the cross-section varies linearly from a to b. The resistivity of the material is ρ. Assuming that b - a << l, find the resistance of the conductor.
Figure 32.E1
Ans : Let us consider a small element strip of length dx at a distance x from one end, as shown below.

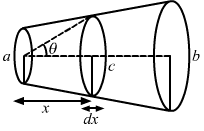
Let the resistance of the small element strip be dR. Let the radius at that point be c .
Then, the resistance of this small strip,
`` \,\mathrm{\,d\,}R=\frac{\rho \,\mathrm{\,d\,}x}{\,\mathrm{\,\pi \,}{c}^{2}}...\left(\,\mathrm{\,i\,}\right)``
`` \,\mathrm{\,tan\theta \,}=\frac{c-\,\mathrm{\,a\,}}{x}=\frac{\,\mathrm{\,b\,}-\,\mathrm{\,a\,}}{L}``
`` \Rightarrow \frac{c-\,\mathrm{\,a\,}}{x}=\frac{\,\mathrm{\,b\,}-\,\mathrm{\,a\,}}{L}``
`` \Rightarrow L\times \left(c-\,\mathrm{\,a\,}\right)=x\times \left(\,\mathrm{\,b\,}-\,\mathrm{\,a\,}\right)``
`` \Rightarrow Lc-\,\mathrm{\,La\,}=xb-xa``
`` ``
Differentiating w.r.t to x, we get:
`` \,\mathrm{\,L\,}\frac{\,\mathrm{\,d\,}c}{\,\mathrm{\,d\,}x}-0=\,\mathrm{\,b\,}-\,\mathrm{\,a\,}``
`` dx=\frac{Ldc}{\left(b\mathit{-}a\right)}...\left(\,\mathrm{\,ii\,}\right)``
Substituting the value of dx in equation (i), we get:
`` \,\mathrm{\,d\,}R=\frac{\rho L\,\mathrm{\,d\,}c}{\,\mathrm{\,\pi \,}{c}^{2}\left(b-a\right)}``
`` \,\mathrm{\,d\,}R=\frac{\rho L}{\,\mathrm{\,\pi \,}\left(b-a\right)}·\frac{\,\mathrm{\,d\,}c}{{c}^{2}}``
`` ``
Integrating dR from a to b, we get:
`` {\int }_{0}^{R}dR=\frac{\rho L}{\,\mathrm{\,\pi \,}\left(\mathit{b}\mathit{-}\mathit{a}\right)}{\int }_{a}^{b}\frac{\,\mathrm{\,d\,}c}{{c}^{2}}``
`` \Rightarrow R=\frac{\rho L}{\,\mathrm{\,\pi \,}\left(\mathit{b}\mathit{-}\mathit{a}\right)}{\left[\frac{-1}{c}\right]}_{a}^{b}``
`` =\frac{\rho L}{\,\mathrm{\,\pi \,}\left(\mathit{b}\mathit{-}\mathit{a}\right)}\left(\frac{-1}{\,\mathrm{\,b\,}}-\frac{-1}{\,\mathrm{\,a\,}}\right)``
`` =\frac{\rho L}{\,\mathrm{\,\pi ab\,}}``
Page No 198:

Qstn #11
A copper wire of radius 0.1 mm and resistance kΩ is connected across a power supply of 20 V.
Ans : Given:
Radius of the wire, r = 0.1 mm = 10^-4 m
Resistance, R = 1 kΩ = 10³ Ω
Voltage across the ends of the wire, V = 20 V