NEET-XII-Physics
32: Electric Current in Conductors
- #10Figure (32.E1) shows a conductor of length l with a circular cross-section. The radius of the cross-section varies linearly from a to b. The resistivity of the material is ρ. Assuming that b - a << l, find the resistance of the conductor.
Figure 32.E1Ans : Let us consider a small element strip of length dx at a distance x from one end, as shown below.
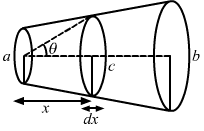
Let the resistance of the small element strip be dR. Let the radius at that point be c .
Then, the resistance of this small strip,
`` \,\mathrm{\,d\,}R=\frac{\rho \,\mathrm{\,d\,}x}{\,\mathrm{\,\pi \,}{c}^{2}}...\left(\,\mathrm{\,i\,}\right)``
`` \,\mathrm{\,tan\theta \,}=\frac{c-\,\mathrm{\,a\,}}{x}=\frac{\,\mathrm{\,b\,}-\,\mathrm{\,a\,}}{L}``
`` \Rightarrow \frac{c-\,\mathrm{\,a\,}}{x}=\frac{\,\mathrm{\,b\,}-\,\mathrm{\,a\,}}{L}``
`` \Rightarrow L\times \left(c-\,\mathrm{\,a\,}\right)=x\times \left(\,\mathrm{\,b\,}-\,\mathrm{\,a\,}\right)``
`` \Rightarrow Lc-\,\mathrm{\,La\,}=xb-xa``
`` ``
Differentiating w.r.t to x, we get:
`` \,\mathrm{\,L\,}\frac{\,\mathrm{\,d\,}c}{\,\mathrm{\,d\,}x}-0=\,\mathrm{\,b\,}-\,\mathrm{\,a\,}``
`` dx=\frac{Ldc}{\left(b\mathit{-}a\right)}...\left(\,\mathrm{\,ii\,}\right)``
Substituting the value of dx in equation (i), we get:
`` \,\mathrm{\,d\,}R=\frac{\rho L\,\mathrm{\,d\,}c}{\,\mathrm{\,\pi \,}{c}^{2}\left(b-a\right)}``
`` \,\mathrm{\,d\,}R=\frac{\rho L}{\,\mathrm{\,\pi \,}\left(b-a\right)}·\frac{\,\mathrm{\,d\,}c}{{c}^{2}}``
`` ``
Integrating dR from a to b, we get:
`` {\int }_{0}^{R}dR=\frac{\rho L}{\,\mathrm{\,\pi \,}\left(\mathit{b}\mathit{-}\mathit{a}\right)}{\int }_{a}^{b}\frac{\,\mathrm{\,d\,}c}{{c}^{2}}``
`` \Rightarrow R=\frac{\rho L}{\,\mathrm{\,\pi \,}\left(\mathit{b}\mathit{-}\mathit{a}\right)}{\left[\frac{-1}{c}\right]}_{a}^{b}``
`` =\frac{\rho L}{\,\mathrm{\,\pi \,}\left(\mathit{b}\mathit{-}\mathit{a}\right)}\left(\frac{-1}{\,\mathrm{\,b\,}}-\frac{-1}{\,\mathrm{\,a\,}}\right)``
`` =\frac{\rho L}{\,\mathrm{\,\pi ab\,}}``
Page No 198: