32: Electric Current In Conductors : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

32: Electric Current in Conductors

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #11
Consider the following two statements:
(A) Kirchhoff’s junction law follows from conservation of charge.
(B) Kirchhoff’s loop law follows from conservative nature of electric field.
(a) A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) A and B are wrong.
digAnsr: a
Ans :
(a) A and B are correct.
According to Kirchhoff's junction law, the net charge coming towards a point should be equal to the net charge going away from that point in the same time. It follows from the principle of conservation of charge.
The loop law follows from the fact that electrostatic force is a conservative force and the work done by it in any closed path is zero.
Page No 197:

Qstn #12
Two non-ideal batteries are connected in series. Consider the following statements:
(A) The equivalent emf is larger than either of the two emfs.
(B) The equivalent internal resistance is smaller than either of the two internal resistances.
(a) A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) A and B are wrong.
digAnsr: b
Ans : (b) A is correct but B is wrong.
Let the emfs of the batteries be e₁ and e₂, and their respective resistances be r₁ and r₂.
Since the batteries are connected in series, the equivalent emf will be the sum of the emf of the two batteries ( e = e₁ + e₂) .
Thus, e > e₁ and e > e₂
Thus, the equivalent emf is larger than either of the two emfs. Hence, statement A is correct.
Since the batteries are connected in series, the equivalent internal resistance (r) of the combination will be the sum of the internal resistance of the two batteries ( r = r₁ + r₂).
r > r₁ and r > r₂
Thus, the equivalent internal resistance is greater that either of the two resistances. Hence, statement B is wrong.
Page No 197:

Qstn #13
Two non-ideal batteries are connected in parallel. Consider the following statements:
(A) The equivalent emf is smaller than either of the two emfs.
(B) The equivalent internal resistance is smaller than either of the two internal resistances.
(a) A and B are correct.
(b) A is correct but B is wrong.
(c) B is correct but A is wrong.
(d) A and B are wrong.
digAnsr: c
Ans : (c) B is correct but A is wrong.
The equivalent emf `` {\epsilon }_{0}`` , when two non-ideal batteries of emfs `` {\epsilon }_{1}`` and `` {\epsilon }_{2}`` and internal resistances r₁ and r₂ respectively are connected in parallel to each other, is given by:
`` {\epsilon }_{0}=\frac{{\epsilon }_{1}{r}_{1}+{\epsilon }_{2}{r}_{2}}{{r}_{1}+{r}_{2}}``
Thus, the equivalent emf is greater than either of the emfs. Thus, statement A is wrong.
For the parallel combination of the batteries of internal resistance r₁ and r₂, the equivalent internal resistance r is given as
`` r=\frac{{r}_{1}{r}_{2}}{{r}_{1}+{r}_{2}}``
Thus, the value of the resultant resistance is even smaller than either resistance.
Page No 197:

Qstn #14
The net resistance of an ammeter should be small to ensure that
(a) it does not get overheated
(b) it does not draw excessive current
(c) it can measure large currents
(d) it does not appreciably change the current to be measured
digAnsr: d
Ans : (d) it does not appreciably change the current to be measured
The ammeter is connected in series with the circuit to measure the net amount of current flowing through the circuit. If the net resistance of the ammeter is high, then the amount of current that the circuit draws will have error. Hence, we cannot accurately measure the amount of current that the circuit draws from the voltage source. Hence, the net resistance or the equivalent resistance of an ammeter should be small enough to ensure that it does not appreciably change the current to be measured.
Page No 197:

Qstn #15
The net resistance of a voltmeter should be large to ensure that
(a) it does not get overheated
(b) it does not draw excessive current
(c) it can measure large potential differences
(d) it does not appreciably change the potential difference to be measured
digAnsr: d
Ans : (d) it does not appreciably change the potential difference to be measured
To measure potential difference across any circuit element, the voltmeter is connected in parallel to that circuit element. Let R_eq be the equivalent resistance of the voltmeter and V be the potential difference across the voltmeter.
Then, the current through the voltmeter, i = `` \frac{V}{{R}_{eq}}``
Hence, the deflection in the voltmeter is proportional to the current i and, hence, proportional to V. However, when the voltmeter is used in a circuit, its resistance R_eq is connected in parallel to some circuit element. This might change the overall resistance of the circuit and, hence, the current. Consequently, the potential difference to be measured is also changed. To minimise the error due to this, the equivalent resistance R_eq of the voltmeter should be large. When a large resistance is connected in parallel to a small resistance, the equivalent resistance is only slightly less than the smaller one.
Page No 197:

Qstn #16
Consider a capacitor-charging circuit. Let Q₁ be the charge given to the capacitor in a time interval of 10 ms and Q₂ be the charge given in the next time interval of 10 ms. Let 10 μC charge be deposited in time interval t₁ and another 10 μC charge be deposited in the next time interval t₂.
(a) Q₁ > Q₂, t₁ > t₂
(b) Q₁ > Q₂, t₁ < t₂
(c) Q₁ < Q₂, t₁ > t₂
(d) Q₁ < Q₂, t₁ < t₂
digAnsr: b
Ans : (b) Q₁ > Q₂, t₁ < t₂
The charge Q on the plates of a capacitor at time t after connecting it in a charging circuit,
`` Q=\epsilon C(1-{e}^{-t/RC})``,
where
ε = emf of the battery connected in the charging circuit
C = capacitance of the given capacitor
R = resistance of the resistor connected in series with the capacitor
The charge developed on the plates of the capacitor in first 10 mili seconds is given by
`` {Q}_{1}=\epsilon C(1-{e}^{-10\times {10}^{-3}/RC})``
The charge developed on the plates of the capacitor in first 20 mili seconds is given by
`` Q\text{'}=\epsilon C(1-{e}^{-20\times {10}^{-3}/RC})``
The charge developed at the plates of the capacitor in the interval t = 10 mili seconds to 20 mili seconds is given by
`` {Q}_{2}=Q\text{'}-{Q}_{1}``
`` {Q}_{2}=\left[\epsilon C(1-{e}^{-20\times {10}^{-3}/RC})\right]-\left[\epsilon C(1-{e}^{-10\times {10}^{-3}/RC})\right]``
`` \Rightarrow {Q}_{2}=\left[\epsilon C({e}^{-10\times {10}^{-3}/RC}-{e}^{-20\times {10}^{-3}/RC})\right]``
`` \Rightarrow {Q}_{2}=\left[\epsilon C\left({e}^{-10\times {10}^{-3}/RC}\right)(1-{e}^{-10\times {10}^{-3}/RC})\right]``
`` ``
Comparing Q₁with Q₂
`` {Q}_{1}=\epsilon C(1-{e}^{-10\times {10}^{-3}/RC}),{Q}_{2}=\epsilon C{e}^{-10\times {10}^{-3}/RC}(1-{e}^{-10\times {10}^{-3}/RC})``
`` \frac{{Q}_{1}}{{Q}_{2}}=\frac{1}{{e}^{-10\times {10}^{-3}/RC}}``
`` {e}^{-10\times {10}^{-3}/RC}<1``
`` \therefore {Q}_{1}>{Q}_{2}``
For second part of the question
10 μC charge be deposited in a time interval t₁ and the next 10 μC charge is deposited in the next time interval t₂.
The time taken for 10 μC charge to develop on the plates of the capacitor is t₁
`` 10\,\mathrm{\,\mu C\,}=\epsilon C(1-{e}^{-{t}_{1}/RC})`` ...(1)
The time taken for 20 μC charge to develop on the plates of the capacitor is t'
`` 20\,\mathrm{\,\mu C\,}=\epsilon C(1-{e}^{-{t}_{2}/RC})`` ....(2)
Dividing (2) by (1)
`` \frac{20\,\mathrm{\,\mu C\,}}{10\,\mathrm{\,\mu C\,}}=\frac{\epsilon C(1-{e}^{-{t}_{2}/RC})}{\epsilon C(1-{e}^{-{t}_{1}/RC})}``
`` 2=\frac{(1-{e}^{-{t}_{2}/RC})}{(1-{e}^{-{t}_{1}/RC})}``
`` 2(1-{e}^{-{t}_{1}/RC})=(1-{e}^{-{t}_{2}/RC})``
`` {e}^{-{t}_{2}/RC}=2{e}^{-{t}_{1}/RC}-1``
Taking natural log both side,
`` \frac{{t}_{2}}{RC}=\,\mathrm{\,ln\,}\left(2\right)+\frac{{t}_{1}}{RC}``
`` \Rightarrow ``t₁ < t₂
Page No 197:

#
Section : iii

Qstn #1
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure (32-Q1). The two stops at the left ensure that the electron beam has a uniform cross-section.
(a) The speed of the electrons is more at B than at A.
(b) The electric current is from left to right.
(c) The magnitude of the current is larger at B than at A.
(d) The current density is more at B than at A.
Figure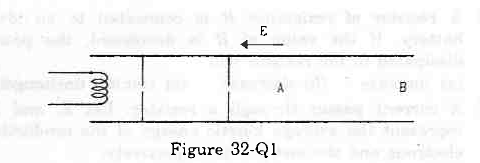
digAnsr: a
Ans : (a) The speed of the electrons is more at B than at A.
Let the potentials at A and B be V_A and V_B.
As potential, `` E=-\frac{dV}{dr}`` ,
potential increases in the direction opposite to the direction of the electric field.
Thus, V_A < V_B
Potential energy of the electrons at points A and B:
U_A= `` -``eV_A
U_B= `` -``eV_B
Thus, U_A> U_B
Let the kinetic energy of an electron at points A and B be K_Aand K_B respectively.
Applying the principle of conservation of mechanical energy, we get:
U_A+ K_A = U_B+ K_B
As, U_A> U_B,
K_A < K_B
Therefore, the speed of the electrons is more at B than at A.
Page No 197:

Qstn #2
A capacitor with no dielectric is connected to a battery at t = 0. Consider a point A in the connecting wires and a point B between the plates.
(a) There is no current through A.
(b) There is no current through B.
(c) There is a current through A as long as the charging is not complete.
(d) There is a current through B as long as the charging is not complete.
digAnsr: b,c
Ans : (b) There is no current through B.
(c) There is a current through A as long as the charging is not complete.
As the capacitor is connected to the battery at t = 0, current flows through the wire up to the time the capacitor is charged. As the capacitor is completely charged, the potential difference across the capacitor is equal to the terminal potential of the battery. So, the current stops flowing and does not pass through the point between the plates of the capacitor, as there is no medium for the flow of charge.
Page No 197:

Qstn #3
When no current is passed through a conductor,
(a) the free electrons do not move
(b) the average speed of a free electron over a large period of time is zero
(c) the average velocity of a free electron over a large period of time is zero
(d) the average of the velocities of all the free electrons at an instant is zero
digAnsr: c,d
Ans : (c) the average velocity of a free electron over a large period of time is zero
(d) the average of the velocities of all the free electrons at an instant is zero
When no current is passed through a conductor, it means that there is no net charge transfer through it. The free electrons are in random motion. The net charge transfer through the cross-section of the conductor is zero. As there is no net charge transfer at any instant, it means that the average of the velocities of all the free electrons at an instant is zero. If we see the motion of each electron as its motion is random and there is no net transfer of charge. Thus, it can be concluded that the average velocity of a free electron over a large period of time is zero.
Page No 197:

Qstn #4
Which of the following quantities does not change when a resistor connected to a battery is heated due to the current?
(a) Drift speed
(b) Resistivity
(c) Resistance
(d) Number of free electrons
digAnsr: d
Ans : (d) Number of free electrons
As the resistor connected to the battery is heated, the thermal energy of the electrons increases. Thus, the relaxation time of the electrons will decrease and so will the drift velocity. Resistivity is inversely proportional to the relaxation time; thus, resistivity will increase with decrease in relaxation time. Therefore, resistance will also change. The number of electrons in a resistor will remain same.
Page No 197:

Qstn #5
As the temperature of a conductor increases, its resistivity and conductivity change. The ratio of resistivity to conductivity
(a) increases
(b) decreases
(c) remains constant
(d) may increase or decrease, depending on the actual temperature
digAnsr: a
Ans : (a) increases
Resistivity (ρ) of a conductor is the reciprocal of the its conductivity(σ). Thus,
`` \rho =\frac{1}{\sigma }``
The ratio of the resistivity and the conductivity,
`` \frac{\rho }{\sigma }=\frac{\rho }{1/\rho }={\rho }^{2}``
As resistivity increases with temperature, the square of resistivity will also increase. Hence, the ratio of resistivity and conductivity will increase with increase in temperature.
Page No 197:

Qstn #6
A current passes through a wire of non-uniform cross-section. Which of the following quantities are independent of the cross-section?
(a) The charge crossing in a given time interval
(b) Drift speed
(c) Current density
(d) Free-electron density
digAnsr: a,d
Ans : (a) The charge crossing in a given time interval
(d) Free-electron density
Drift speed and current density are inversely proportional to the area of cross-section of a wire. Thus, they are dependent on the cross-section. The charge crossing in a given time interval is independent of the area of cross-section of the wire. Free electron density is the total number of free electrons per unit volume of the wire. The density of free electrons depends on the distribution of the free electrons throughout the volume of the wire. It does not depend on the cross-section of the wire.
Page No 197:

Qstn #7
Identify the correct options.
(a) An ammeter should have small resistance.
(b) An ammeter should have large resistance.
(c) A voltmeter should have small resistance.
(d) A voltmeter should have large resistance.
digAnsr: a,d
Ans : (a) An ammeter should have small resistance.
(d) A voltmeter should have large resistance.
The ammeter is connected in series in the circuit whose current is to be measured. If the net resistance of the ammeter is high, then the amount of current that the circuit draws will have error . So, we won't be able to accurately measure the amount of current that the circuit draws from the voltage source. Thus, it should have a small resistance.
To measure the potential difference across any circuit element, the voltmeter is connected in parallel to that circuit element. If the resistance of the voltmeter is large, then maximum voltage drop occurs across the voltmeter and it will measure the correct value of the potential.
Page No 198:

Qstn #8
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
digAnsr: a,b,c,d
Ans : (a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
The charge (Q) on the capacitor at any instant t,
`` Q=CV(1-{e}^{-t/RC})``,
where
C = capacitance of the given capacitance
R = resistance of the resistor connected in series with the capacitor
RC = (10 × 10³) × (500 × 10^{`` -``6}) = 5 s
The charge on the capacitor in the first 5 seconds,
`` {Q}_{0}=CV(1-{e}^{-5/5})=CV\times 0.632``
`` ``
The charge on the capacitor in the first 10 seconds,
`` {Q}_{1}=CV(1-{e}^{-10/5})``
`` {Q}_{1}=CV(1-{e}^{-2})=0.864\times CV``
Charge developed in the next 5 seconds,
Q' = Q₁ `` -`` Q₀
Q' = CV(0.864 `` -`` 0.632) = 0.232 CV
The charge on the capacitor in the first 55 seconds,
`` {Q}_{2}=CV(1-{e}^{-55/5})``
`` {Q}_{2}=CV(1-{e}^{-11})=0.99\times CV``
Charge developed in the next 50 seconds,
Q' = Q₂ `` -`` Q₀
Q' = CV(0.99 `` -`` 0.632) = 0.358 CV
Charge developed in the first 505 seconds,
`` {Q}_{3}=CV(1-{e}^{-500/5})=CV(1-{e}^{-100})\approx CV``
Charge developed in the next 500 seconds,
Q' = CV (1`` -`` 0.632) = 0.368 CV
Thus, the charge developed on the capacitor in the first 5 seconds is greater than the charge developed in the next 5,50, 500 seconds.
Disclaimer : Out of the four given options, two options are same.
Page No 198: